Matematik

Del 3: Mobilmasten

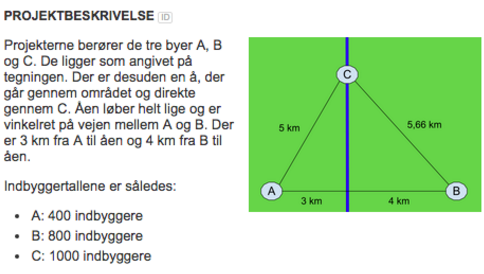
11. april 2019 af az97 - Niveau: B-niveau

Kommunen skal finde den optimale placering til en ny mobilmast. Mobilmasten skal placeres langs vejen mellem A og B, men spørgsmålet er, hvor på strækningen?

For at få mest glæde af masten skal den placeres således, at gennemsnittet af kvadraterne på borgernes afstand til masten bliver mindst mulig.

"Gennemsnittet af kvadraterne på borgernes afstand" bestemmes ved, at man for hver borger tager afstanden til masten, sætter denne afstand i anden og derefter tager gennemsnittet for alle borgerne.

- Opstil en matematisk model, der angiver gennemsnittet af kvadraterne på borgernes afstand alt efter placeringen af masten på vejen mellem A og B. Kald mastens afstand til A for x. Husk at tage hensyn til byernes forskellige indbyggertal, men antag at byerne ikke har nogen udstrækning.

- Bestem den optimale placering for masten.

Vedhæftet fil: Skærmbillede 2019-04-11 kl. 17.41.55.png

Brugbart svar (0)

Svar #1
12. april 2019 af PeterValberg

Jeg indsætter lige dit billede, det gør det nemmere at hjælpe

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (3)

Svar #2
12. april 2019 af PeterValberg

Masten er placeret på linjen AB
Den lodrette afstand fra C til linjen AB kan bestemmes til 4 (vha. Pythagoras)

Afstanden fra A til masten er: $x$
Afstanden fra B til masten er: $7-x$
Afstanden fra C til masten er: $\sqrt{4^2+(3-x)^2}=\sqrt{x^2-6x+25}$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #3
12. april 2019 af PeterValberg

"Gennemsnittet af kvadraterne på borgernes afstand" bestemmes ved, at man for hver borger tager afstanden til masten, sætter denne afstand i anden og derefter tager gennemsnittet for alle borgerne.

Den sætning er lidt kryptisk og kan fortolkes på forskellige måder,
men hvis den tolkes som summen af alle borgers afstande til masten
kvadreret (sat i anden) og divideret med det samlede antal borgere, fås:

$f(x)=\frac{\left(400x+800(7-x)+1000\sqrt{x^2-6x+25}\,\right)^2}{400+800+1000}$

hvilket sikkert kan reduceres lidt

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #4
29. januar 2020 af shifu1

hej

Brugbart svar (2)

Svar #5
08. maj 2020 af frozone7

#2
Masten er placeret på linjen AB
Den lodrette afstand fra C til linjen AB kan bestemmes til 4 (vha. Pythagoras)

Afstanden fra A til masten er: $x$
Afstanden fra B til masten er: $7-x$
Afstanden fra C til masten er: $\sqrt{4^2+(3-x)^2}=\sqrt{x^2-6x+25}$

Peter Valberg, kan du forklare hvorfor afstanden fra C til masten giver dette?

Brugbart svar (1)

Svar #6
21. oktober 2020 af Ladora (Slettet)

For at bestemme den optimale placering for masten, hvad gør jeg så?

Skriv et svar til: Del 3: Mobilmasten

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.