Matematik
Bestem projektionen af punktet A(7,20) på linjen l.
Hejsa. Er der nogle kloge hoveder der kan hjælpe mig med denne opgave? God aften :-)
Svar #2
21. maj 2019 af jonathanbanke
Ja netop denne opgave, er der en der kan hjælpe mig med den? :-)
Svar #3
21. maj 2019 af AMelev
Punktet A skal projiceres vinklret på linjen l, så projektionen PA kan bestemmes som skæringspunktet mellem linjen l og linjen m gennem A vinkelret på l.
Lettest at benytte ligning for l og parameterfremstilling for m.
Svar #5
21. maj 2019 af oppenede
Det er uddybet her: https://www.studieportalen.dk/forums/thread.aspx?id=1889183
Svar #6
22. maj 2019 af AMelev
Metoderne i linket er andre end den foreslåede i #1, men lige så brugbare.
Ad #1 Bestem ligningen for l.
Normalvektoren for l er retningsvektor for m, da de skal være ortogonale.
Bestem parameterfremstillingen for m med som retningsvektor og A som punkt.
Indsæt parameterudtrykkene for x og y i ligningen for l og løs ligningen mht. t.
Indsæt så den fundne t-løsning i parameterfremstillingen for at bestemme PA.
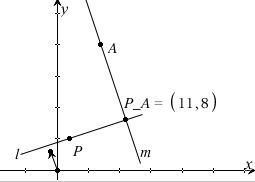
Du kan også benytte konstruktion i dit geometriværktøj til at finde projektionen, men husk, du skal dokumentere fremgangsmåden.
Skriv et svar til: Bestem projektionen af punktet A(7,20) på linjen l.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



