Matematik

Største og mindste værdi i definitionsmængde

10. oktober 2019 af Jepp5220 - Niveau: Universitet/Videregående

Har funktionen $f(x,y)=xy-x,$ som er defineret i

$D=0<=y<=2-x^2$

Jeg skal gøre rede for at f antager såvel en største som en mindste værdi på D, og derefter udregne dem. Hjælp please, har kigget på det i nogle timer nu og er mere forvirret end da jeg startede

Brugbart svar (0)

Svar #1
10. oktober 2019 af mathon

$\small \begin{array}{lllll} \textup{indre punkter:}&f_x=\frac{\mathrm{d} f}{\mathrm{d} x}=y-1\qquad f_y=\frac{\mathrm{d} f}{\mathrm{d} y}=x\\\\ &f_x=f_y=0\\\\ &y-1=0\Leftrightarrow y=1\\\\ &x=0\\\\ &f_{xx}=f_{yy}=0\\\\ &f_{xy}=1\\\\ &f_{xx}=f_{yy}=0\\\\ &f_{xx}\cdot f_{yy}-{f_{xy}}^2=0-1<0\Rightarrow \textup{ saddelpunkt i (0,1)}\\\\\\\\ \textup{gr\ae nsepunkter:}&0\leq y\leq 2-x^2\\\\ \textup{maximumspunkt:}&(0,2)\\\\ \textup{minimumspunkter:}&(-\sqrt{2},0)\textup{ og }(\sqrt{2},0) \end{array}$

Brugbart svar (0)

Svar #2
10. oktober 2019 af Soeffi

#0.

Vedhæftet fil:Skærmbillede 2019-10-10 kl. 10.58.33.png

Svar #3
10. oktober 2019 af Jepp5220

Hvordan udregner du max og minimumspunkterne #1? Er med på hvordan du fandt det kritiske punkt

Svar #4
10. oktober 2019 af Jepp5220

De punkter du gav mig er vel randpunkterne, ikke nødvendigvis min og max.
Evaluerede mine randpunkter og kritiske punkter, og fandt min værdien til -3,4142, og max til 0,25 i intervallet

Brugbart svar (0)

Svar #5
18. oktober 2020 af Musses

Hvorfor et saddelpunkt og ikke et lokalt minimumspunkt, når f(y) $\geq$ f(x)?

Brugbart svar (1)

Svar #6
23. oktober 2020 af Soeffi

#5. Hvorfor et saddelpunkt og ikke et lokalt minimumspunkt, når f(y) $\geq$ f(x)?

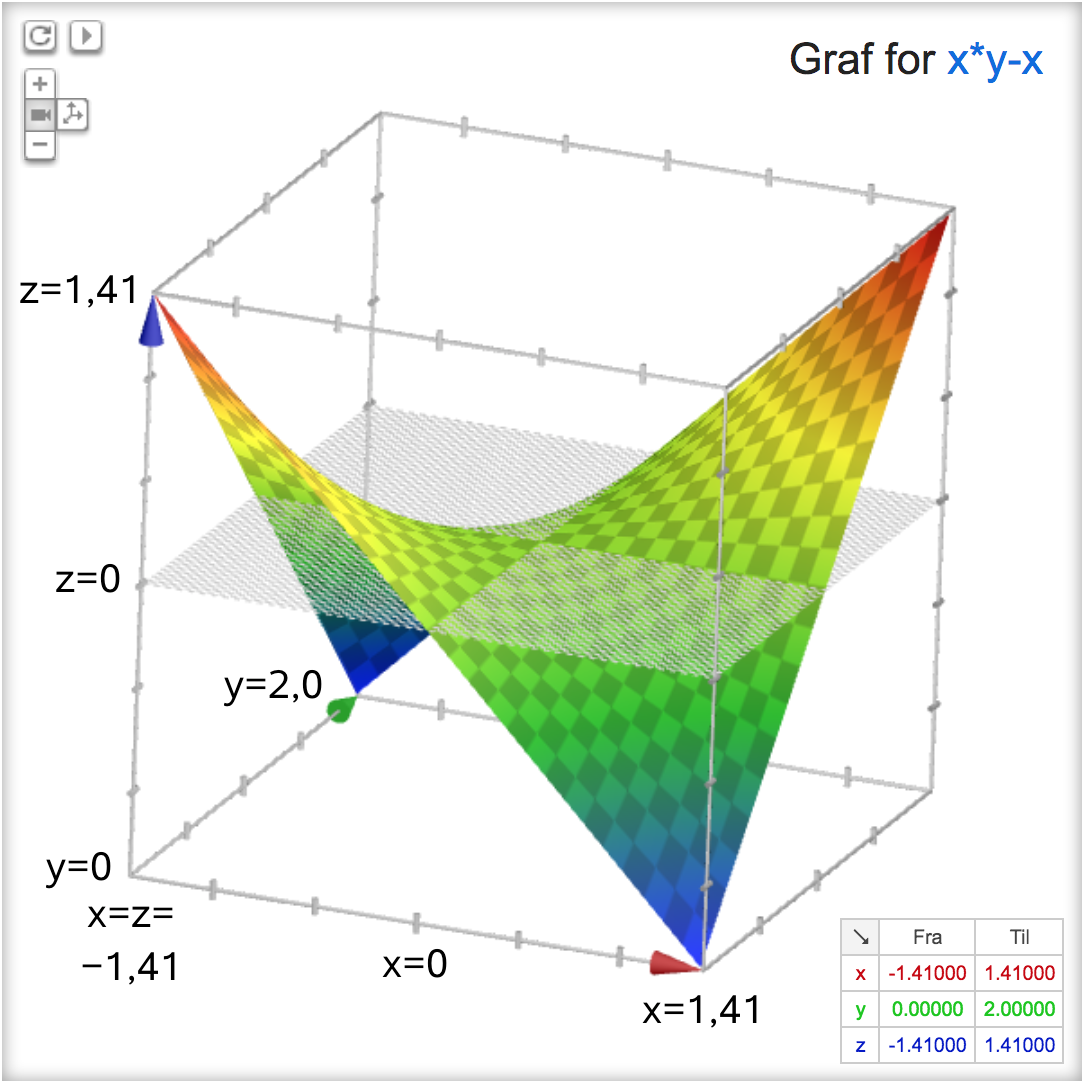
Det er forklaret i #1 og fremgår af grafen i #2...Det sidste: f(x) og f(y) giver ikke mening, da det er en funktion i to variable dvs. f(x,y).

Der er et kritisk punkt for f i punktet (x,y) = (0,1), hvor gradienten for f er (0,0).

Størsteværdien findes i (-√2,0) og mindsteværdien i (√2,0).

Brugbart svar (0)

Svar #7
24. oktober 2020 af Musses

Jeg indså, at jeg var helt galt på den, efter jeg oprettede kommentaren - men da var det for sent at redigere den. Jeg er med nu. Tak for hjælpen :)

Skriv et svar til: Største og mindste værdi i definitionsmængde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.