Matematik

Anvendelser af differentialregning Monotoniforhold

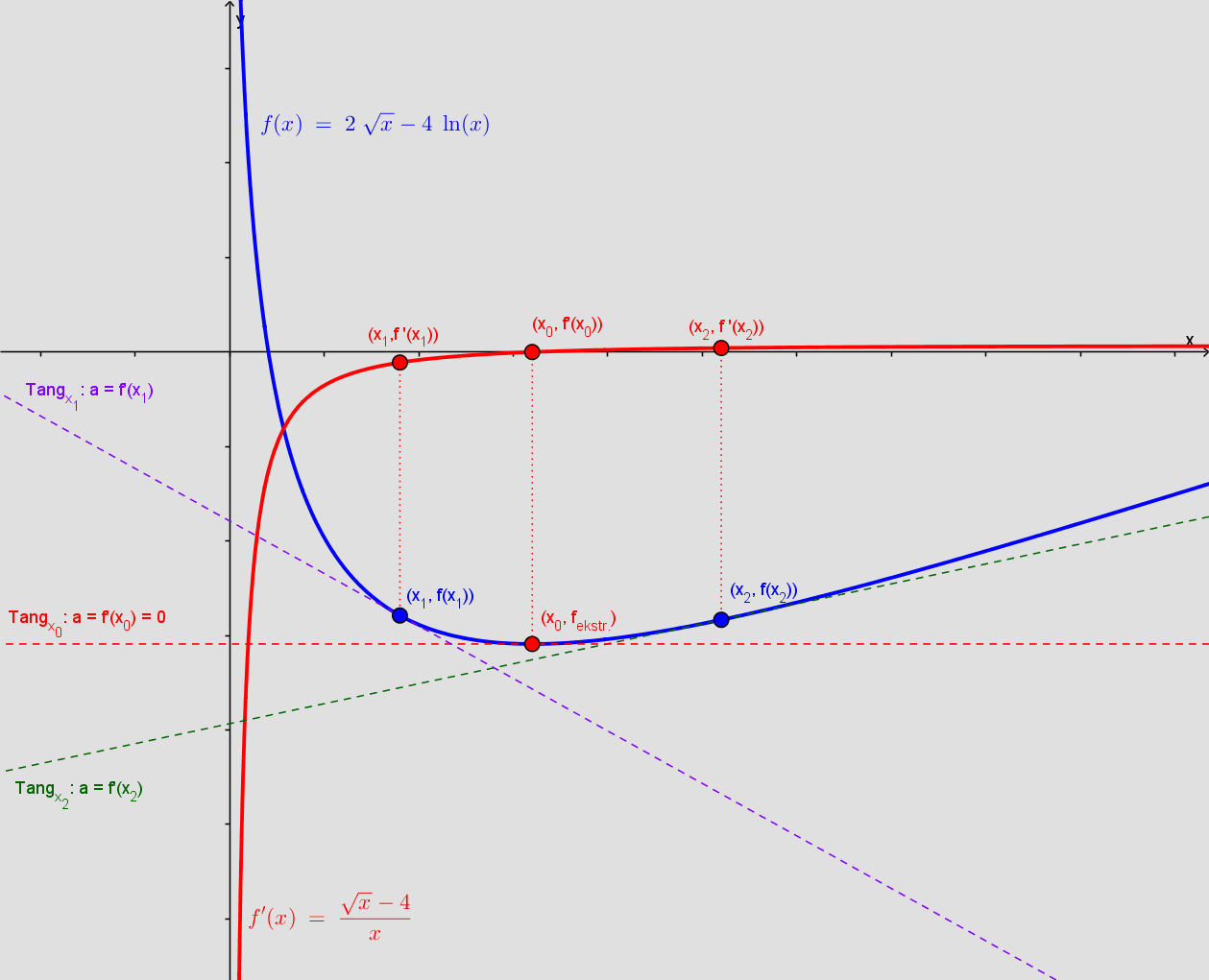
17. november 2019 af signecr - Niveau: B-niveau

betragt funktionen f givet ved f(x)=2√x-4ln(x), x>0

bestem monotioniforholdet for f

på forhånd tak for hjælpen

Brugbart svar (0)

Svar #1
17. november 2019 af ringstedLC

$\begin{align*} f(x) &= 2\sqrt{x}-4\ln(x)\;,\;x>0 \\ f'(x) &= \;? \\ f'(x) &= 0\Rightarrow x_0=\;?\text{ indsat i \textit{f} giver ekstrema} \\ f'(x) &< 0\Rightarrow f\text{ er aftagende} \\ f'(x) &> 0\Rightarrow f\text{ er voksende} \\ f'(x<x_0) &= \;? \\ f'(x>x_0) &= \;? \end{align*}$

Svar #2
17. november 2019 af signecr

det jeg har indtil vidre er f'(x)=1 √x -4/x

ved ikke hvad jeg skal gøre der fra

Brugbart svar (0)

Svar #3
17. november 2019 af ringstedLC

$\begin{align*} f'(x) &= \frac{1}{\sqrt{x}}-\frac{4}{x} \end{align*}$

og så går du til 3. linje i #1.

Svar #4
17. november 2019 af signecr

men skal det ikke isoleres først?

Brugbart svar (0)

Svar #5
17. november 2019 af ringstedLC

#1
$\begin{align*} f(x) &= 2\sqrt{x}-4\ln(x)\;,\;x>0 \\ f'(x) &= \;? \\ f'(x) &= 0\Rightarrow x_0=\;?\text{ indsat i \textit{f} giver ekstrema} \\ f'(x) &< 0\Rightarrow f\text{ er aftagende} \\ f'(x) &> 0\Rightarrow f\text{ er voksende} \\ f'(x<x_0) &= \;? \\ f'(x>x_0) &= \;? \end{align*}$

Se på tangenterne til funktionen. Den tangent, der er parallel med x-aksen, rører der hvor funktionen har ekstremum. Derfor skal du løse f '(x) = 0 for at bestemme x₀, da diff.-kvotienten er hældningen af tangenten.

De to andre tangenters hældning skal ikke bestemmes, blot skal det undersøges om deres hældning er positiv eller negativ, hvilket gøres ved at indsætte en værdi x₁ < x₀, henholdsvis en værdi x₂ > x₀? i f '(x) og beregne funktionsværdien.

Vedhæftet fil:__0.png

Skriv et svar til: Anvendelser af differentialregning Monotoniforhold

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.