Forklar hvorfor en differentialkvotient er defineret som en grænseværdi

Måske for den går lige til grænsen for, hvad en nævner må.
Den må jo ikke blive = 0.

En ret linjes hældningskoefficient er forholdet mellem to y-værdiers differens og de tilsvarende to
x-værdiers differens. Nu er hældningskoefficienten overalt den samme for en ret linje, men for en
ikke-lineær funktion vil kurvehældningen variere med kurveforløbet. Ved så at sige at erstatte en
meget snæver omegn omkring et kurvepunkt med et kort linjestykke vil hældningskoefficienten
beregnes som ovenfor anført. Nu har de reelle tal imidlertid den egenskab, at de ligger tæt, d.v.s.,
at der til ethvert positivt a og b, hvor a < b , vil der eksistere et c , således at a < c < b. Vi må da yder-
ligere indsnævre omegnen omkring kurvepunktet, således at intervallet indsnævres så meget,
at det kun indeholder kurvepunktet. Det er det der sker ved    hvor Δx → 0.
En kvotient er resultatet af en division, og en differentialkvotient er resultatet af divisionen, når Δx gøres
vilkårlig lille.

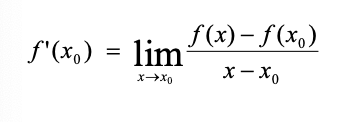
Når du bestemmer en diff.-kvotient er det geometrisk det samme som at bestemme hældningen af en uendelig kort tangent. I formlen:

skal de to differencer så være uendelig små pga. Pythagoras, dog må nævneren ikke være 0. Disse to betingelser for nævneren kan beskrives/er defineret som en grænseværdi (lim = limit ≈ grænse).

Pythagoras' er ikke involveret ved grænseundersøgelsen af differenskvotienter, men er det, hvis vi f.eks. skal
bestemme skrå asymptoter.