Matematik

Bevis for linære- og eksponentielle funktioners vækstegenskaber

20. januar 2020 af joseflahlou (Slettet)

Er der nogen, der kan forklare disse to sætninger i detaljer. Har fundet beviset på internettet, men forstår ikke, hvad der sker fra linje til linje. Billede er vedhæftet.

Sætningerne:

Eksponentielle funktioner har den vækstegenskab, at hvis x ændres med en absolut tilvækst, så ændres
f(x) med relativ tilvækst.

For linære funktioner gælder, hvis x-værdien vokser med delta x, så vokser y-værdien med a gange delta x.

Vedhæftet fil: Capture.JPG

Brugbart svar (0)

Svar #1
20. januar 2020 af ringstedLC

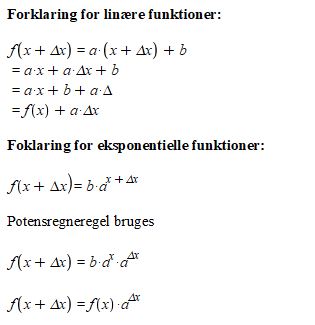
$\begin{align*} \text{Line\ae r\,funktion }f(x) &= {\color{DarkGreen} a\cdot x+b} \\ f(x+\Delta x) &= a\cdot (x+\Delta x)+b\;,\;\Delta x\text{ er en absolut v\ae rdi} \\ &= a\cdot x+a\cdot \Delta x+b\;,\;a\text{ ganges ind i parentesen} \\ &= {\color{DarkGreen} a\cdot x+b}+a\cdot \Delta {\color{Red} x}\;,\;\text{ der\,mangler desv\ae rre et }x \\ &= f(x)+a\cdot \Delta x \\\\ \text{Eksponentiel funktion }f(x) &= {\color{Magenta} b\cdot a^{x}} \\ f(x+\Delta x) &= b\cdot a^{x\,+\Delta x}\;,\;\Delta x\text{ er en absolut v\ae rdi} \\ &= {\color{Magenta} b\cdot a^{x}}\cdot x^{\,\Delta x}\;,\;r^{s\,+\,t}=r^s\cdot r^t \\ &= f(x)\cdot a^{\,\Delta x} \end{align*}$

Forskellen er at funktionerne fremskrives med henholdsvis "+ a · tilvkst. i x" og "· a^{tilvkst. i x}".

Gennemse al den hjælp du har fået til emnet, måske specielt opgaven med afskrivning på en maskine ( se: https://www.studieportalen.dk/forums/thread.aspx?id=1933127)

Svar #2
20. januar 2020 af joseflahlou (Slettet)

Jeg har indsat det manglende x, men hvad sker der i den linje?

Brugbart svar (0)

Svar #3
20. januar 2020 af ringstedLC

Ikke andet end at leddene flyttes rundt, så substitutionen med f(x) bliver tydeligere.

Skriv et svar til: Bevis for linære- og eksponentielle funktioners vækstegenskaber

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.