Fysik

Astronomi. afstand til månen og dens radius

18. februar 2020 af TheMathNerd - Niveau: B-niveau

God aften Studieportals medlemmer

Jeg har desværre udfordringer med en astronomi opgave, men kan ikke se I har den kategori indsat her så jeg har reflekteret på at astronomi og fysik kan nogenlunde sammensættes i et.

Jeg har denne opgave (Jeg kan ikke umiddelbart sige om dette hører til matematik eller ej, men jeg tager det med et gran salt)

Og inkl opgaven fortalte min lærer at:
Bestem ud fra oplysningerne afstanden til Månen. ( D.v.s. afstanden c på figuren)

Vil sætte meget stor pris på jeres engagerede og ambitiøse bud.

Vedhæftet fil: Astronomi Hr. Larsen.png

Svar #1
18. februar 2020 af TheMathNerd

Havde også dette til at tilføje med Månens radius så håber ikke det bliver det helt store besvær ellers må I undskylde mig at det ikke er min intention at udnytte jeres pragtfulde viden til mit eget forbrug, men til læring og forbedrelse.

Vedhæftet fil:Astronomi Hr Larsen Radius.png

Brugbart svar (0)

Svar #2
18. februar 2020 af ringstedLC

#1: Opgaven passer fint til "Fysik".

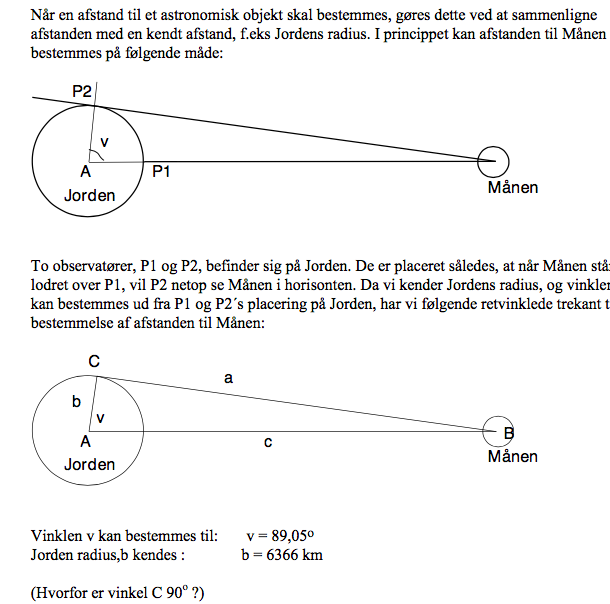
Brug trigonometri for den retvinklede trekant.

Brugbart svar (1)

Svar #3
18. februar 2020 af ringstedLC

og for:

Svar #4
19. februar 2020 af TheMathNerd

Matematik er ikke min helt stærke side så håber du kan hjælpe mig hen ad vejen

Brugbart svar (1)

Svar #5
19. februar 2020 af ringstedLC

Generelt for en retvinklet trekant ABC, hvor vinkel C = 90º:

$\begin{align*} \sin(A) &= \frac{\text{modst\aa ende katete}}{\text{hypotenusen}} =\frac{a}{c} \\ \cos(A) &= \frac{\text{hosliggende katete}}{\text{hypotenusen}} =\frac{b}{c} \\ \tan(A) &= \frac{\text{modst\aa ende katete}}{\text{hosliggende katete}} =\frac{a}{b} \end{align*}$

#2: Du har vinkel v og en hosliggende katete. Hypotenusen c er afstanden mellem Jordens- og Månens centre:

$\begin{align*} \cos(v) &= \frac{\text{hosliggende katete}}{\text{hypotenusen}} =\frac{b}{c} \\ c &= \frac{b}{\cos(v)} \\ c &= \frac{6366}{{\cos(89.05}^{\circ})}=\;?\text{ km} \end{align*}$

#3: Her kender du en anden vinkel v og har nu beregnet hypotenusen c. Den modstående katete b er Månens radius:

$\begin{align*} \sin(v) &= \frac{\text{modst\aa ende katete}}{\text{hypotenusen}} =\frac{b}{c} \\ b &=\sin(v)\cdot c \\ b &= \sin(0.25^{\circ})\cdot c=\;?\text{ km} \end{align*}$

Svar #6
19. februar 2020 af TheMathNerd

#5 om #2 383959,6 km

#5 om #3 sin (0,25^o) * 383959,6 = 1675,334

Er det sådan?

Brugbart svar (0)

Svar #7
19. februar 2020 af ringstedLC

Ja. Prøv også at svare på hvorfor vinkel C = 90º

Svar #8
19. februar 2020 af TheMathNerd

#7
Ja. Prøv også at svare på hvorfor vinkel C = 90º

Linjen tangerer med cirklen som fra analytisk plangeometri ville være defineret som retvinklet.

Men jeg forstår ikke den med vinkel diameter og vil vide kan du hjælpe hengiveligt vis med den.

Brugbart svar (1)

Svar #9
19. februar 2020 af ringstedLC

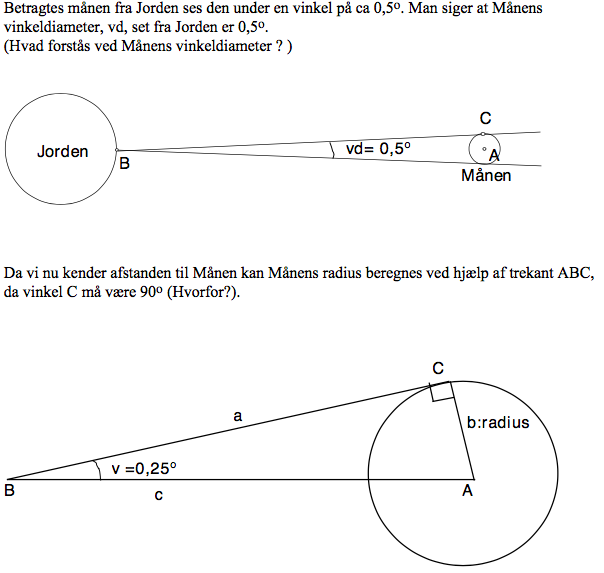
De to tangenter som lige præcis rammer dit ene øje, danner vd. Den er opgivet til ca. 0.5º, da afstanden mellem Jorden og Månen varierer. Derfor er vd mindst, når Månen er længst væk fra Jorden.

Skriv et svar til: Astronomi. afstand til månen og dens radius

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.