Matematik
Har svært ved at forstå og løse opgaven
(graferne ligger i vedhæftet)
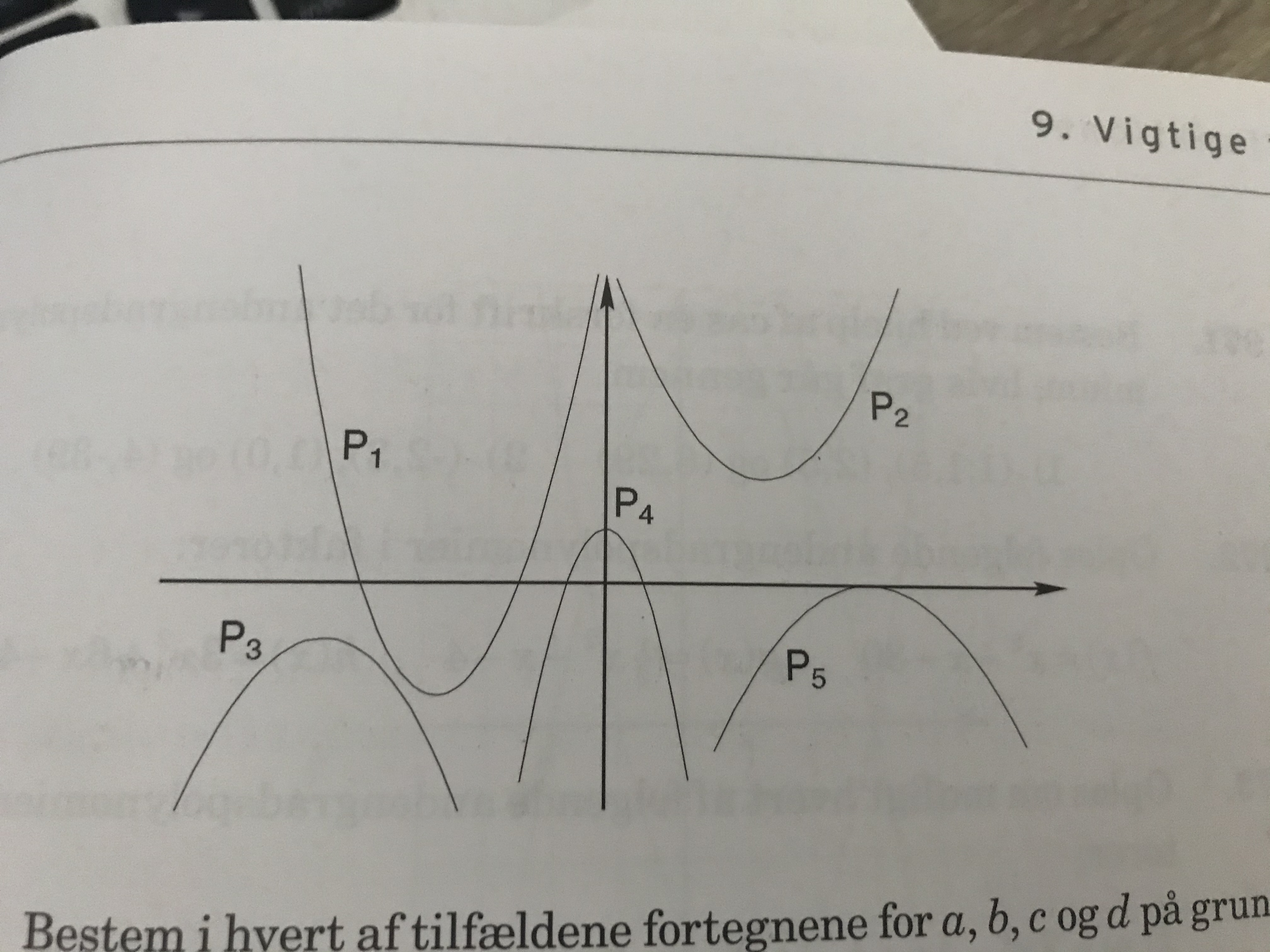
Bestem i hvert af tilfældene fortegnene for a, b, c og d på grundlag af graferne på figuren. Idet andengradskoefficienterne betegnes med a1, a2, a3, a4 og a5 skal de sættes op i rækkefølge med den største først.
Svar #1
17. marts 2020 af AMelev
Betydning af
a: a > 0 ~ grene opad, a > 0 ~ grene nedad, jo større |a| des stejlere graf
b: Hældning af tangenten i (0,p(0))
c: Graf gennem (0,c)
d: d > 0 ~ 2 nulpunkter, d = 0 ~ 1 nulpunkt, d < 0 ~ Ingen nulpunkter
Start fra en ende af.
Svar #2
17. marts 2020 af javannah5
Hvordan finder jeg fortegnene for a, b, c og d ved at kigge på graferne og hvilke grafer tilhører hvilke bogstaver?
Og hvad menes med ‘ Idet andengradskoefficienterne betegnes med a1, a2, a3, a4 og a5’?
Svar #3
17. marts 2020 af ringstedLC
Andengradskoefficienten er koefficienten på variablen x2. Det er fortegnet af den, der bestemmer om grenene vender op eller ned. Og det er værdien af den, der bestemmer, hvor stejl grafen er.
Eksempler: P4 har negativt a
Svar #4
17. marts 2020 af javannah5
Men igen til det første spørgsmål Hvordan finder jeg fortegnene for a, b, c og d ved at kigge på graferne og hvilke grafer tilhører hvilke bogstaver? for jeg har ikke forstået det første svar der blev skrevet øverst oppe.
Svar #5
17. marts 2020 af ringstedLC
Ja, så a'erne er på plads. Dog mangler du at indeksere dem efter størrelse; a1, a2 ..., så det polynomium med størst a-værdi opskrives:
b, c og d i #1 er sikkert ment som almen info
b: Hældningen af grafens tangent (en ret linje) i (0,P(0)) som er et punkt på y-aksen. Læg linealen som tangent i skæringen og afgør om hældningen er positiv eller negativ.
c: Funktionsværdien af P(0), - altså y-værdien af skæringen med y-aksen.
d: Diskriminantens fortegn giver antallet af skæringspunkter (nulpunkter) med x-aksen.
Svar #6
17. marts 2020 af javannah5
P1= a1x^2+b1x+c1
P2=a2x^2+b2x+c2
P3= a3x^2+b3x+c3
P4= a4x^2+b4x+c4
P5= a5x^2+b5x+c5
(Skal a i P3 og P5 være negativt eller ej)
Og hvad er fortegnene for a, b, c og d ud fra graferne
Men kan du også skrive til sidst hvilke polynom(graf) er til hvert bogstav
Svar #7
17. marts 2020 af ringstedLC
#6 Ok polynomium med størst a-værdi skal det så se sådan her ud:
P1= a1x^2+b1x+c1
P2=a2x^2+b2x+c2
P3= a3x^2+b3x+c3
P4= a4x^2+b4x+c4
P5= a5x^2+b5x+c5
(Skal a i P3 og P5 være negativt eller ej)
Og hvad er fortegnene for a, b, c og d ud fra graferne
Men kan du også skrive til sidst hvilke polynom(graf) er til hvert bogstav
#5 rettelse: Grafen med størst a værdi opskrives:
1. Graferne P1 og P2 er opskrevet korrekt fordi a1 > a2, men ved resten skal du lige overveje betydningen af, at a er en negativ værdi. Det vil sige, at når P4 er stejlest og vender grenene nedad, så må
2. Du skal ikke bestemme fortegn for de andre konstanter.
3. Det giver ingen mening; P1 er parablen øverst til venstre osv.
Svar #8
17. marts 2020 af javannah5
Hvad er svaret til P5, da a er negativ?
Svar #10
18. marts 2020 af javannah5
Og forstår ikke hvordan A1 man være større end A2 da 2 er større end 1
Svar #11
18. marts 2020 af AMelev
Mht. fortegn for a, b, c og d
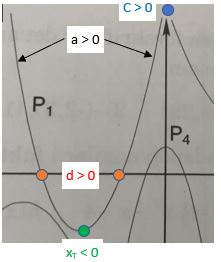
a: Grenene opad, så a1 > 0
c: P1 skærer y-aksen i (0,c1), som ligger over x-aksen, så c1 > 0
d: Der er to nulpunkter (skæringspunkter med x-aksen), så d1 > 0
b: Jeg havde overset, at du har angivet 1g, så den med tangenten kan du nok ikke bruge, men så kan du bruge nedenstående:
Toppunktets 1.koordinat xT = -b/(2a) ⇔ -2xT·a = b.
xT1 er negativ, og a1 er positiv, så fortegn for b1 er "- · - · + = +", altså b1 > 0.
Svar #12
18. marts 2020 af ringstedLC
#10 Men hvordan finder jeg hvilket har størst fx mellem P3 og P5
Og forstår ikke hvordan A1 man være større end A2 da 2 er større end 1
Lad P3 "glide" over i P5, så deres toppunkter er sammenfaldende og se hvilken graf, der er stejlest.
"A1" skal være a1; skriv rigtigt. "1" er et indeks og ikke en værdi. Men den parabel, der har den største værdi af a, skal have koefficienten a1. Og det er den parabel, der vender grenene opad (fordi pos. > neg.) og er stejlest.
Svar #13
18. marts 2020 af javannah5
Hvis P1 er c>0 fordi den skærer y-aksen i 0 vil det så sige at P2 også har c>0 fordi det gøre den også
Og hvad er P4, P3 og P5 fortegn for c?
Svar #14
18. marts 2020 af AMelev
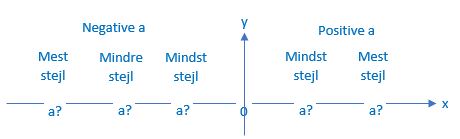
P1 og P2 har grenene opad, så a1 og a2 er positive.
Afgør, hvilken af de to grafer der er stejlest. Angiv derudfra, om a1 eller a2 er størst
P3, P4 og P5 har grenene nedad, så a3, a4 og a5 er negative.
Gør dig de samme overvelser som ved P1 og P2.
Svar #15
18. marts 2020 af AMelev
#13
Kig på tegningen! Du kan da se, at 1.koordinaten til toppunktet er negativ. Det er ovenikøbet markeret.
# 10
1, 2, 3 osv er bare nummereringer (indekser) af de forskellige parabler - så man kan kende dem fra hinanden på navnet - og dermed også af de tilsvarende koefficienter. Man kunne også have kaldt dem PJensen, PHansen osv., det er bare meget mere besværligt.
Svar #16
18. marts 2020 af javannah5
P1= c>0
P2= c>0
P3= c<0
P4= c<0
P5= c<0
Er alle rigtige eller ej
Og igen kan du forklarer på en nemmere måde hvordan man fonder fortegnene for d og b til graferne
Svar #17
18. marts 2020 af ringstedLC
#14: "Angiv derudfra, om a1 eller a2 er størst". Nej, da:
#0 P1,P2, P3, P4, og P5 er grafer for forskellige andengradspolynomier, der kan skrives på formen P(x) = ax2+ bx + c med diskriminanten d.
(graferne ligger i vedhæftet)
Bestem i hvert af tilfældene fortegnene for a, b, c og d på grundlag af graferne på figuren. Idet andengradskoefficienterne betegnes med a1, a2, a3, a4 og a5 skal de sættes op i rækkefølge med den største først.
vel må forstås sådan, at a1 er størst og er koefficienten i den parabel P?, der har grenene opad og er stejlest. Tilsvarende hører a5 til den parabel, der har grenene nedad og er stejlest.
Svar #18
18. marts 2020 af AMelev
#17 Jeg læser det, som det står i #6, at a1 hører til P1 osv.. Der står jo, at a1, a2, a3, a4 og a5 skal ordnes efter størrelse med den største først.
#16 P4 er ikke rigtig. Den skærer jo y-aksen på den positive del.
Beklager, jeg kan ikke forklare fortegn for b og d på en nemmere måde.
Se på graferne og se, hvor mange gange den enkelte graf skærer/rører 2.aksen og benyt det til at bestemme fortegn for d, jf #1 (og figur i #11)
Find toppunkterne for den enkelte graf og se, om 1.koordinaten xT er negativ, 0 eller positiv. Benyt dette og fortegnet for den tilsvarende a-værdi til at bestemme fortegn for b = -2xT·a, jf #11.
Husk fortegnsreglerne: "+ · + = +", "+ · - = -" og "- · - = +"
Svar #19
18. marts 2020 af ringstedLC
#6 Ok polynomium med størst a-værdi skal det så se sådan her ud:
P1= a1x^2+b1x+c1
P2=a2x^2+b2x+c2
P3= a3x^2+b3x+c3
P4= a4x^2+b4x+c4
P5= a5x^2+b5x+c5
(Skal a i P3 og P5 være negativt eller ej)
Og hvad er fortegnene for a, b, c og d ud fra graferne
Men kan du også skrive til sidst hvilke polynom(graf) er til hvert bogstav
#18: Ja, men det er jo kun fordi P1 og P2 har den største henholdsvis den næststørste værdi af a. a4 er ikke den fjerdestørste a-værdi.
Skriv et svar til: Har svært ved at forstå og løse opgaven
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






