Matematik

hjælp til Matematik

29. marts 2020 af maria2016 - Niveau: B-niveau

Hey, Jeg har prøvet at løse den her opgave,men får ikke det samme resultat som facit.

Opgaven er, en funktion f er givet ved f(x) = (x+6) * ( x-2) * (x-8)

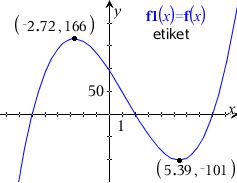
Jeg skal benyt f´(x) til at bestemme monotoniforholdene for f. Jeg har prøvet at løse den på geogebra men får ikke det rigtige resultat, som er f er voksende for xx≤ -2,72 og for x ≥ 5,39. f har et lokalt maksimum i (-2,72;166) og et lokalt (5,39 ;-101)

Desuden ved jeg ikke hvordan jeg skal bestemme en ligning for de tangenter til grafen for f, der har en hældningskoefficient på 4. I facit står der y = 4x + 177 og y= 4x - 123

Brugbart svar (0)

Svar #1
29. marts 2020 af ringstedLC

GG kan differentiere for dig. I "Input:" skrives: f ' og tryk <Enter>. Det giver:

$\begin{align*} f'(x) &= 3x^2-8x-44 \end{align*}$

Dens nulpunkter:

- Værktøjet "Rødder" anvendt på f ' giver skæringspunkter m. x-aksen, hvis f ikke har nogle intervaller. Ellers må man "trylle" lidt.

- Værktøjet "Ekstremum" anvendt på f giver min./maks.-punkter. Deres x-værdi er også løsninger til f ' = 0.

- I "Input:" skriv: løs og vælg forslaget. <Ligning> udfyldes med f '=0 og tryk <Enter>. Det giver en liste med de numeriske løsninger.

- I "Input:" skriv: ber og vælg forslaget Beregn( <Ligning> ). <Ligning> udfyldes og du får en liste med eksakte løsninger.

- Værktøjet "Skæringsværktøj" bruges på f ' og x-aksen.

Alle metoderne giver:

$\begin{align*} f'(x) &= 0 \\ x &= \left\{\begin{matrix} \frac{-2\sqrt{37}+4}{3}\approx -2.72 \\\\ \frac{2\sqrt{37}+4}{3}\approx 5.39 \end{matrix}\right. \end{align*}$

Brugbart svar (0)

Svar #2
29. marts 2020 af peter lind

Hvis du har fået et galt resultat i geogebra, må du have lavet en fejl ved ingivelse af data.

Find f'(x) og løs ligninge f'(x) = 4. De to løsninger angiver for hvilket x0 den tangenten berører grafeen for f(x)

Svar #3
29. marts 2020 af maria2016

Super tusind tak for hjælpen, det giver mere mening nu :)

Brugbart svar (0)

Svar #4
29. marts 2020 af AMelev

a) Hvad har du f '(x) til? Du skulle gerne have f '(x) = 3x²- 8x - 44, som har nulpunkterne x = 2.72184 og x=5.38851.
På f-grafen kan du så se, at der er lok. max i x = 2.72 og lok. min i x = 5.39.

b) Når tangenten skal have en hældningskoefficient på 4, skal f '(x₀) = 4.
Løs ligningen mht. x0, så har du de to røringspunkters 1.koordinater. Indsæt i tangentligningen FS side 23 (121).

Vedhæftet fil:Udklip.JPG

Svar #5
29. marts 2020 af maria2016

ser dette rigtig ud(tangentligningen):

3x^2 - 8x - 44

3*4^2 - 8*4 - 44 = 116

f´(x) = 3x^4-1 - 8*4x^4-1 - 44 = 3x^3 -32^3

Brugbart svar (0)

Svar #6
29. marts 2020 af ringstedLC

Absolut ikke, for nu at sige pænt.

Du har bestemt den afledede af et 3. gradspolynomium til at være et andet 3. gradspolynomium.

Løs ligningen f '(x₀) = 4 betyder:

$\begin{align*} f'(x_0)=4 &= 3{x_0}^2-8x_0-44 \\ 0 &= 3{x_0}^2-8x_0-48 \\ x_0 &= \;? \\ y &= f'(x_0)\,(x-x_0)+f(x_0) \\ y &= 4\cdot (x-x_0)+f(x_0) \end{align*}$

Svar #7
29. marts 2020 af maria2016

skal jeg nu ikke indsætte 4 på alle x´s plads

Brugbart svar (0)

Svar #8
29. marts 2020 af mathon

$\small \begin{array}{lllll}&\textup{solve}\left (f{\, }'(x)=4,x \right )\\\\ &x=\left\{\begin{array}{lll} \frac{4-4\sqrt{10}}{3}\approx -2.883037\\ \frac{4+4\sqrt{10}}{3}\approx 5.549704 \end{array}\right.\\\\\textup{tangent}_1\textup{:} &y=4\cdot (x- (-2.883037))+f( -2.883037)\\\\&y=4x+177\\\\\\ \textup{tangent}_2\textup{:} &y=4\cdot (x-5.549704)+f(5.549704)\\\\&y=4x-123 \end{array}$

Brugbart svar (0)

Svar #9
29. marts 2020 af AMelev

#5 Nej, du skal løse ligningen f '(x₀) = 4 ikke beregne f '(4) (som iøvrigt er -28 og ikke 116).
f '(x₀) = 4 ⇔ 3x₀²- 8x₀ - 44 = 4 ⇔ x₀= .... eller x₀ = ......

Svar #10
29. marts 2020 af maria2016

Mange tak for hjælpen alle sammen :)

Brugbart svar (0)

Svar #11
29. marts 2020 af ringstedLC

#7
skal jeg nu ikke indsætte 4 på alle x´s plads

Når du sætter en værdi ind i en funktion, giver funktionen en funktionsværdi:

$\begin{align*} f(x) &= 2x+4 \\ f(\text{tal}) &= 2\cdot \text{tal}+4=\text{funktionsv\ae rdi} \end{align*}$

Grafisk: Fra tal på x-aksen gås op/ned til grafen og y-værdien aflæses.

Når du har en funktionsværdi til en funktion, kan du finde den x-værdi, der giver funktionsværdien. Det gøres ved at løse ligningen:

$\begin{align*} f(x)=funktionsv\ae rdi &= 2x+4 \\ x &= \;? \end{align*}$

Grafisk: Fra funktionsværdi på y-aksen gås v./h. til grafen og x-værdien aflæses.

Svar #12
29. marts 2020 af maria2016

Yes det giver rigtig godt mening

Skriv et svar til: hjælp til Matematik

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.