Matematik

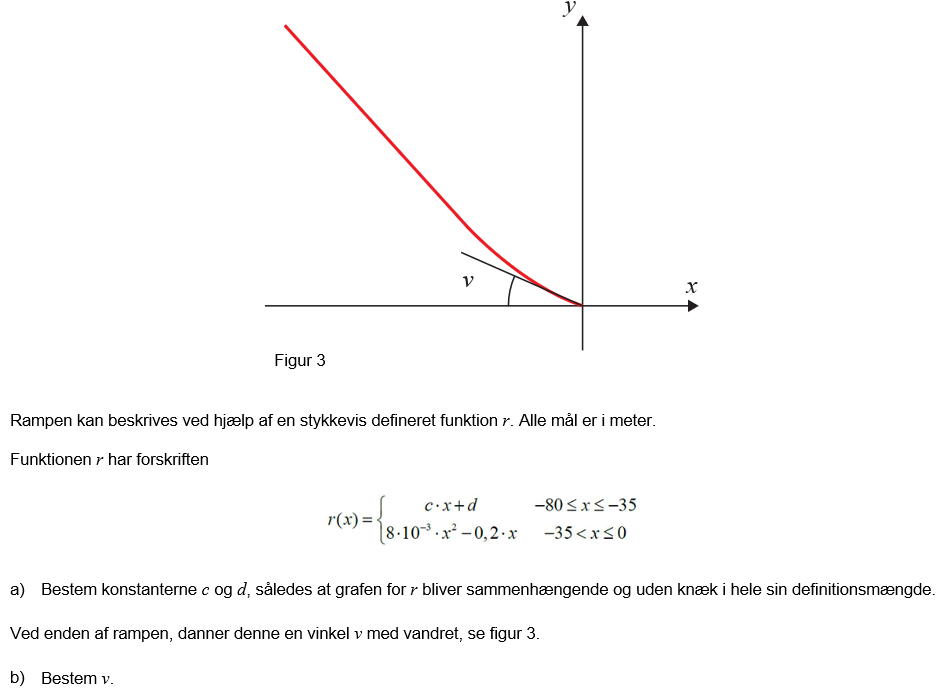
stykkevise funktion

31. marts 2020 af DeepOcean - Niveau: B-niveau

Hej..

jeg har brug for lidt hjælp for at bestemme konstant a og b i stykkevise funktion i opgave a . se venlig på vedhæfte fil.

jeg er klare ove at man skal løse den som ligningsystem med to ubekendte men jeg har ikke værdien for y ..

i opgave b : forselår jeg at jeg differentialler funktion når -35<x<0 og jeg får først grad ligning og sætter jeg den lige med nul og løse den i hensyn til x ,så hvis jeg tager tan^(-1) (x) = vinkel ..har jeg gjorde rigtigt ?

Vedhæftet fil: Mat-Opgave.PNG

Brugbart svar (0)

Svar #1
31. marts 2020 af mathon

Brugbart svar (2)

Svar #2
31. marts 2020 af mathon

$\small \begin{array}{llll} a)& c=16\cdot10^{-3}\cdot(-35)-0.2=-0.76 \end{array}$

Brugbart svar (2)

Svar #3
31. marts 2020 af AMelev

De to delfunktioners grafer skal støde sammen i x = -35, da grafen skal være sammenhængende, dvs. at f1(-35) = f2(-35).

Deusde skal grafen være glat, dvs. funktionen skal være differentiabel, så f1'(-35) = f2'(-35).

Start med den sidste ligning og bestem c. Indsæt så i 1. ligning og bestem d.
Eller løs med dit CAS-værktøj som to ligninger med 2 ubekendte.

Svar #4
31. marts 2020 af DeepOcean

Mange tak for jere svar : hvad med opgave b) har i også en ide om den?

Brugbart svar (0)

Svar #5
31. marts 2020 af mathon

$\small \small \begin{array}{llllll}b)&-0.76\cdot (-35)+d=8\cdot 10^{-3}\cdot (-35)^2-0.2\cdot(-35)\\\\ & d=-9.8 \end{array}$

Brugbart svar (0)

Svar #6
31. marts 2020 af AMelev

Tangenthældningen i 0 er f2'(0).
Benyt Tan(v) = a, hvor a er hældningskoefficienten.

Du var sporet, men du skal altså ikke løse f2'(x) = 0, men beregne f2'(0).

Svar #7
31. marts 2020 af DeepOcean

vil du være venlige og forkalre hvorfor du sætte f2`(0) som svar til hældning..,,skal måske regne f2`(-35) som svar til hældning??

Brugbart svar (1)

Svar #8
31. marts 2020 af AMelev

Det er jo tangenten, der udgår fra røringspunktet (0,f2(0)).

Brugbart svar (1)

Svar #9
31. marts 2020 af ringstedLC

Rampen ender i (0,0); der må den have hældningen r '(0). Bemærk: (0,0) er ikke parablens toppunkt.

Svar #10
31. marts 2020 af DeepOcean

Tak for det .Der giver bedre mening nu. men jeg får vinklen -11,30 grad .er det normal man får en negative vinkel?..jeg er klar over at hældning er negative så burde give negative vinkel, men kan vi ser bort fra negative fortegn og skrive at vinklen er bare 11,30 ??

Brugbart svar (1)

Svar #11
31. marts 2020 af ringstedLC

Den anvendte formel giver en vinkel i 1.- eller 4. kvadrant.

Læs op på hvordan tangens ligger i forhold til enhedscirklen.

Svar #12
01. april 2020 af DeepOcean

Tak for det

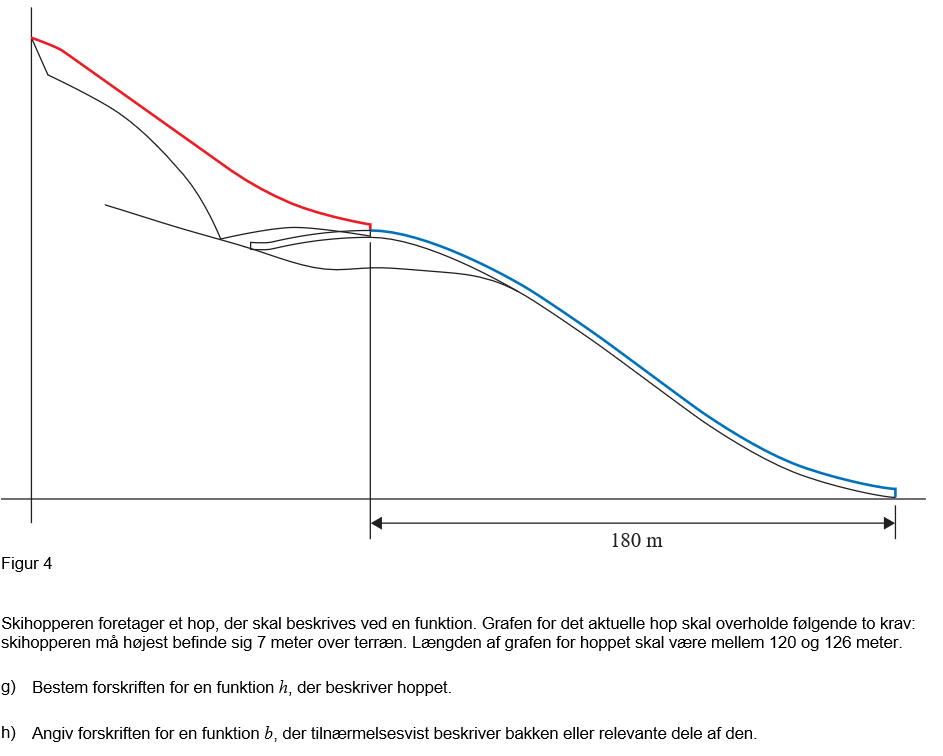
Jeg har en anden spørgsmål som har noget med det først spørgsmål. der drejse sig om jeg skal finde en forktion forskrift for skihoppe. jeg vedhæfte fil og håber at nogle vil bruge tid til læse filen og give mig et godt forslag til det. :)

Det drejser sig om spørgsmål g og h .

Vedhæftet fil:Mat-Opgave-g-h.PNG

Brugbart svar (0)

Svar #13
01. april 2020 af AMelev

Husk: Ny opgave ~ ny tråd.
Ellers risikerer du, at ingen ser det nye spørgsmål, eller at de få, der ser det, ikke kan hjælpe dig.

Brugbart svar (0)

Svar #14
01. april 2020 af ringstedLC

Sammenhængen mellem dette og dit første spørgsmål, er ikke ret tydelig.

Tænk på, at alt du ved efter at have svaret på a) - f), ved vi jo ikke.

Vedhæft hele opgaven med dine svar. Og gør det selvfølgelig i en ny tråd

Svar #15
02. april 2020 af DeepOcean

https://www.studieportalen.dk/forums/thread.aspx?id=1949720
Har lavet nyt tråd og hat upload hele opgave som nævnt før jeg
Har det svært ved opgave g og h
Opgave a til f er lavet

Brugbart svar (0)

Svar #16
13. april 2020 af Jacob881 (Slettet)

Hej :) Hvordan kom du frem til en vinkel på 11.30?

Brugbart svar (0)

Svar #17
13. april 2020 af ringstedLC

#16: Ved at benytte

#6
Tangenthældningen i 0 er f2'(0).
Benyt Tan(v) = a, hvor a er hældningskoefficienten.

Brugbart svar (0)

Svar #18
13. april 2020 af Jacob881 (Slettet)

Så du benytter denne formel?

Vedhæftet fil:mat d.3.PNG

Brugbart svar (0)

Svar #19
13. april 2020 af ringstedLC

eller bare:

$\begin{align*} \tan(v)=a \Rightarrow v &= \tan^{-1}(a) \\ v &= \tan^{-1}\left ( f2'(-35) \right )\;,\;f2(x)=r(x)\;,\;-35\leq x\leq 0 \end{align*}$

Brugbart svar (0)

Svar #20
13. april 2020 af Jacob881 (Slettet)

Hmmm synes jeg får det til 88?

Forrige 1 2 Næste

Der er 27 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.