Fysik

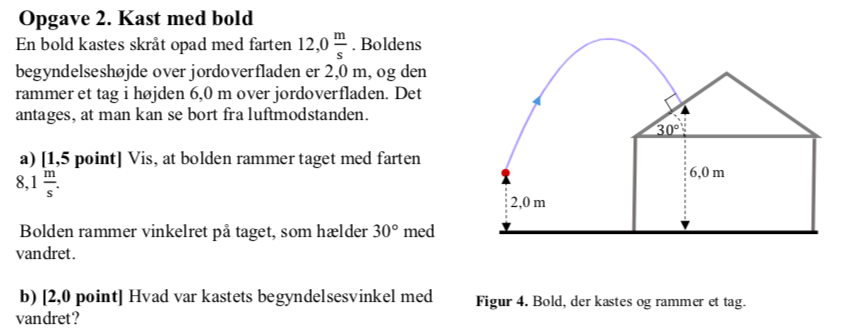
Skrå kast i fysik

01. december 2020 af mariehøns1 (Slettet) - Niveau: B-niveau

Nogen der kan hjælpe med at løse disse to opgaver. Er virkelig gået i stå?

Vedhæftet fil: Skærmbillede 2020-12-01 kl. 12.19.59.png

Brugbart svar (0)

Svar #1
01. december 2020 af Soeffi

Brugbart svar (0)

Svar #2
01. december 2020 af Moderatoren

Skriv hvor du er gået i stå #0

Brugbart svar (0)

Svar #3
01. december 2020 af janhaa

0,5mv₁² + mgh₁ =0,5mv₂² + mgh₂

0,5*12² + 2g = 6g + 0,5v₂²

v₂ = 8,1 (m/s).

Brugbart svar (1)

Svar #4
01. december 2020 af Soeffi

#0. b) Hvis du vælger det punkt, hvor bolden rammer taget, som nulpunkt for koordinatsystemer, så har du en parabel, der kan skrives:

$f(t)=a t^2+bt$

Her er a = -0,5·g = -4,91 og b = -sin(60°)·8,1 = -7,015. Dvs.

$f(t)=-4,91\cdot t^2-7,015\cdot t$

Der gælder, at f'(t₁) = 12·sin(α), hvor α er startvinklen og hvor t₁ er det tidspunkt (før t = 0), hvor bolden er 4 m under nulpunktet.

Man finder t₁:

$f(t_1)=-4,91\cdot t_1^2-7,015\cdot t_1=-4\Rightarrow t_1=-1,8654$

$f'(-1,8654)=11,303$

$12 \cdot sin(\alpha)=11,303\Rightarrow \alpha=70,015^o$

Vedhæftet fil:Untitled1.png

Brugbart svar (0)

Svar #5
01. december 2020 af Soeffi

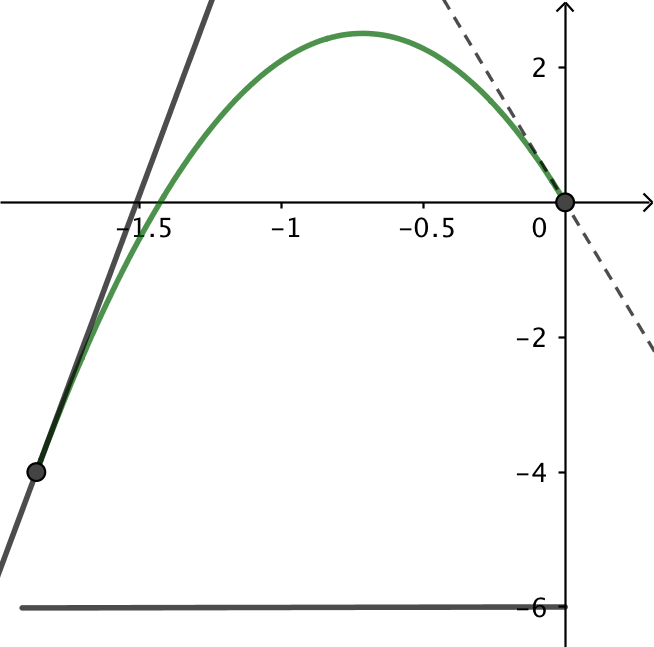
#4 b) Hvis du betragter boldens højde over et punkt, hvor den rammer taget, som funktion af tiden, så får du funktionen:
$f(t)=a t^2+bt$

Bemærk f(t) er ikke højden over jorden som funktion af kastelængden, men højden over taget som funktion af tiden. Den vandrette akse er antal sekunder.

Brugbart svar (0)

Svar #6
02. december 2020 af Soeffi

#4...med enheder og yderligere forklaring:

b)

$f(t)=a t^2+bt$

Her er a = -0,5·g = -4,91m/s² og b = -sin(60°)·(8,1 m/s) = -7,015 m/s. Dvs.

$f(t)=(-4,91\;m/s^2)\cdot t^2-(7,015\;m/s)\cdot t$

Der gælder, at f'(t₁) = (12 m/s)·sin(α), hvor α er startvinklen, og hvor t₁ er det (negative) tidspunkt, hvor bolden er 4 m under nulpunktet. Man finder t₁:

$f(t_1)=(-4,91\;m/s^2)\cdot t_1^2-(7,015\;m/s)\cdot t_1=-4\;m\Rightarrow t_1=-1,8654\;s$

Man finder start-farten i y-aksens retning (længden af y-komposanten til hastighedsvektoren i starten):

$f'(-1,8654\;s)=11,303\;m/s$

Heraf finder man start-vinklen:

$(12\;m/s) \cdot sin(\alpha)=11,303\; m/s\Rightarrow \alpha=70,015^o$

Brugbart svar (0)

Svar #7
02. december 2020 af Soeffi

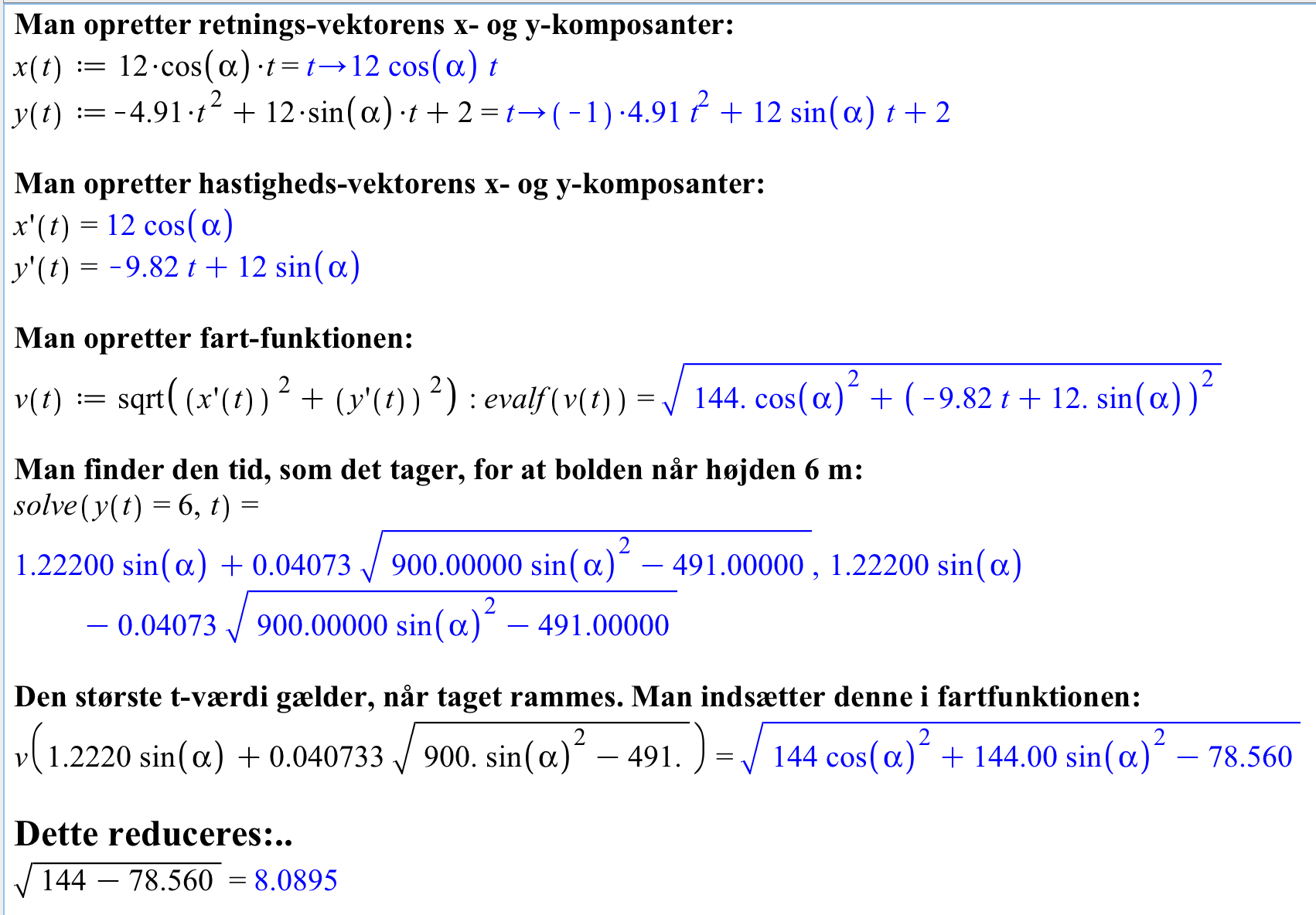
#0. Spørgsmål a) løses nemmest med mekanisk-energi betragtning. Den kan dog også løses med vektorer, hvis man bruger CAS og håndkraft (cos²(x) + sin²(x) = 1):...

Vedhæftet fil:Skærmbillede 2020-12-02 kl. 14.40.05.png

Brugbart svar (0)

Svar #8
07. december 2020 af Soeffi

#0.

Vedhæftet fil:Skærmbillede 2020-12-07 kl. 15.38.16.png

Skriv et svar til: Skrå kast i fysik

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.