Matematik

Højde

27. februar 2021 af august543 - Niveau: A-niveau

Hej.

Jeg har svært ved at løse delopgave b i den vedhæftede fil. Jeg har dog fundet løsningen til opgaven, men forstår dog ikke hvorfor der er regnet som der er gjort. Hvis nogle kunne forklare det step til step, ville det være en stor hjælp:)

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
27. februar 2021 af ringstedLC

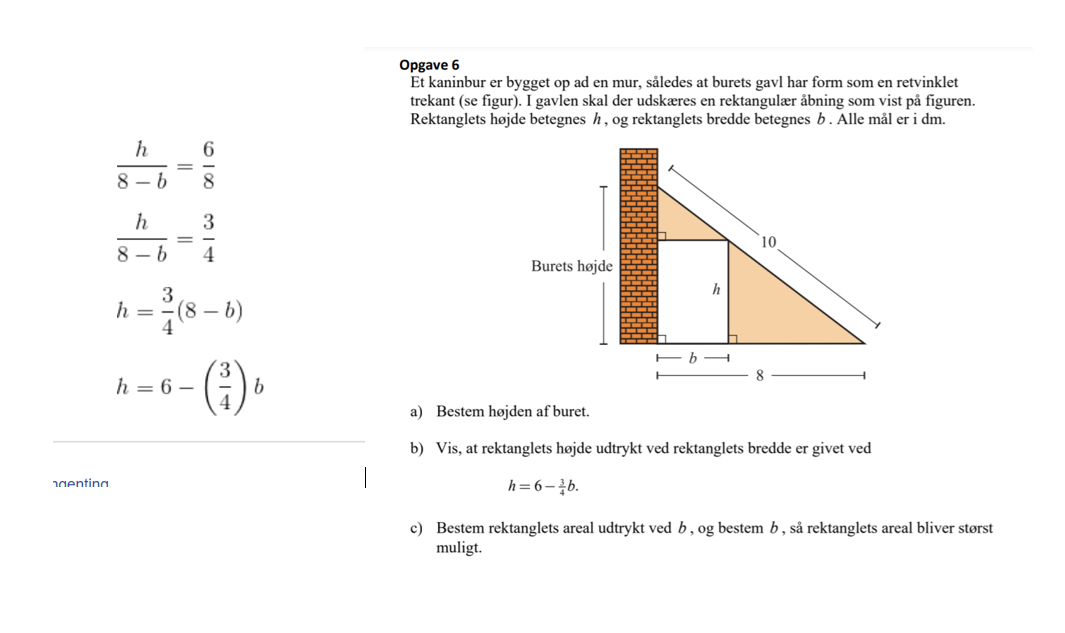
Trekanten, hvor h er den ene katete, er ensvinklet med gavltrekanten. Der gælder:

$\begin{align*} \frac{h}{6} &= \frac{8-b}{8} \\ h &= \frac{6}{8}\cdot (8-b) \end{align*}$

fordi forholdene mellem ensvinklede trekanters sider er lige store.

Svar #2
27. februar 2021 af august543

#1

Trekanten, hvor h er den ene katete, er ensvinklet med gavltrekanten. Der gælder:

$\begin{align*} \frac{h}{6} &= \frac{8-b}{8} \\ h &= \frac{6}{8}\cdot (8-b) \end{align*}$

fordi forholdene mellem ensvinklede trekanters sider er lige store.

hvorfor står der 8-b/8 og hvor kommer 8-tallet fra i nævneren?

Brugbart svar (0)

Svar #3
27. februar 2021 af ringstedLC

Læs om ensvinklede trekanter på https://www.webmatematik.dk/lektioner/7-9-klasse/geometri/ensvinklede-trekanter

Brugbart svar (0)

Svar #4
28. februar 2021 af AMelev

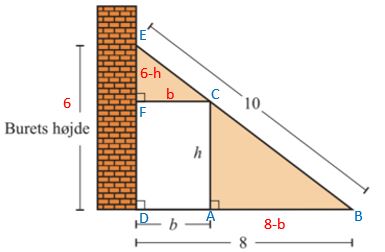
ΔABC og ΔDBE er ensvinklede, så $\frac{|AC|}{|DE|}=\frac{|AB|}{|DB|}$ .
|AC| = h, |DB| = 8, |AB| = |DB| - |DA| = 8 - b og iflg. a) er |DE| = 6

Du kunne også i stedet have kigget på ΔABC og ΔFBE, som også er ensvinklede.
|EF| = |DE| - |DF| =6 - h.
Så havde du fået $\frac{6-h}{h}=\frac{b}{8-b}\Leftrightarrow (6-h)\cdot (8-b)=h\cdot b \Leftrightarrow 48-6b-8h+h\cdot b=h\cdot b\Leftrightarrow$
$48-6b=8h\Leftrightarrow h=\frac{48-6b}{8}=6-\frac{3}{4}b$ .

Vedhæftet fil:Udklip.JPG

Skriv et svar til: Højde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.