Matematik
Skæringspunkter og areal
08. marts 2021 af
Okayyyy
-
Niveau: A-niveau
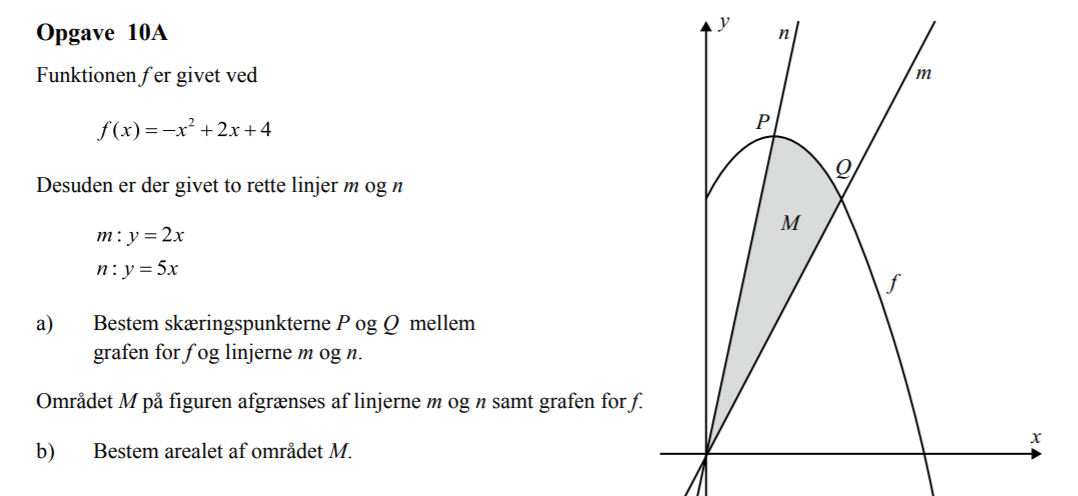
Funktionen f er givet ved f(x)= - x2 + 2x +4. Desuden er der givet to rette linjer m og n
m: y = 2x
n: y = 5x
a) Bestem skæringspukterne P og Q mellem grafen for f og linjerne m og n.
Området M på figuren afgrænses af linjerne m og n amt grafen for f.
b) Bestem arealet af området M
Hvordan løser jeg de to opgaver?
Skriv et svar til: Skæringspunkter og areal
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.