Matematik
Bestem boldens maksimale højde
Opgaven lyder:
En bold kastes lodret op i luften og følger følgende forskrift for højden i meter som funktion af tiden i sekunder;
Først fandt jeg den afledede funktion .
For at finde funktionens ekstrema, må det være dér hvor tangenthældningen er 0, så jeg løste ligningen
Jeg satte derefter værdien for t ind i den afledede funktion for at finde den tilhørende y (meter) værdi til vores t - for at finde koordinatsættet til dette maksimum
Men jeg får det forkerte resultat
Jeg ved ikke om min fremgangsmetode er forkert eller om det er mine mellemberegninger...
Tak på forhånd.
Fremgangsmetoden lyder helt rigtig, måske kan du vise dine mellemberegninger
Svar #3
17. juni 2021 af 1234vedikke
Jeg har et andet spørgsmål...
Vi kan lave fortegnsanalyse for at være sikker på, at det er et maksimum vi har fundet, men er det relevant? Må man egentlig antage, at der er underforstået kun tale om et maksimum eftersom opgaven lyder, at man skal finde boldens maksimale højde, så må man antage, at bolden bliver grebet det samme sted den blev kastet og fx. ikke rammer jorden og hopper op igen...
Eller er det nødvendigt, at lave en fortegnsanalyse?
Svar #4
17. juni 2021 af 1234vedikke
Okay, jeg tror faktisk ikke fortegnanalyse er nødvendigt, fordi vi får kun et ekstrema, så vil det ikke give mening, hvis det var et minimum, for så skulle jeg ikke lave opgaven...
Du har ret i at fordi h'(t)=0 kun har en løsning, så har h(t) kun et ekstrema. Men det kunne være at en del af opgaven var at du kan vise at du forstår hvordan man bestemmer om det er et top eller bund-punkt.
Der er vist noget med at fortegnet foran t^2 afgør om grafen er "glad" eller "sur"
Svar #6
17. juni 2021 af 1234vedikke
Tak for svar! Og ja, man kan enten kigge på fortegnet foran t^2 eller indsætte en værdi som er større eller mindre end t i den afledede funktion - det er dog nok nemmere at gøre det du skriver :D Men i forhold til konteksten i opgaven så står der også, at bolden bliver kastet opad, så på den anden side tror jeg ikke det er så vigtigt alligevel at nævne det. Dog kan jeg kort lige skrive i opgaven og argumentere hvorfor det ikke er nødvendigt - ifølge mig ihvertfald. xD
Svar #7
17. juni 2021 af MountAthos
Til # 0
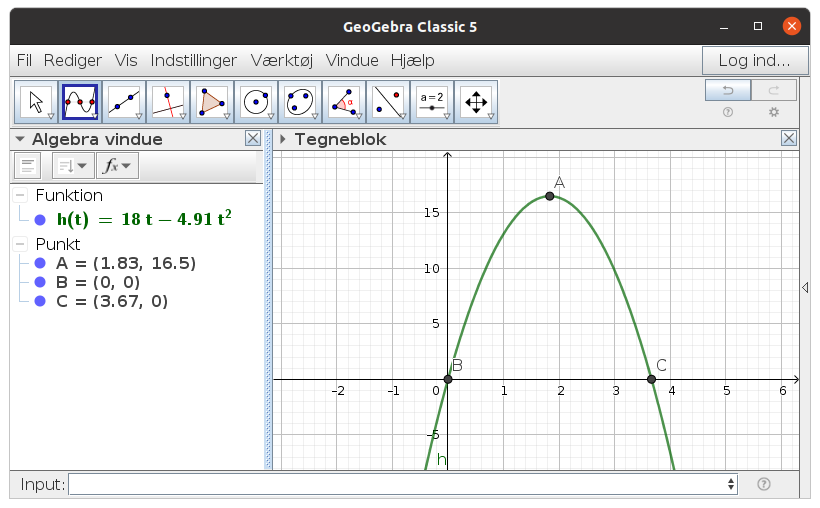
Du kan tjekke dit resultat ved at beregne koordinaterne til grafens toppunkt
h ( t ) = 18 t - 4.91 t2
toppunkt t = - b / 2· a = -(18 /( 2 · 4.91) = 1,8329
indsæt t = 1.8329 i h ( t ) = 18 t - 4.91 t2 så for du 18· 1.8329 - (4.91 · ( 1.8329 )2 ) = 16.5
Toppunkt har koordinaterne x = 1.8329 og y = 16.5
Så boldens maksimale højde er 16.5 meter
En anden mulighed er at tegne grafen
Svar #8
17. juni 2021 af 1234vedikke
#7 Ja, det kunne jeg selvfølgelig også gøre! - Eller hvis man er lidt mere doven af natur, kan man plotte grafen ind i Geogebra - men jeg vidste godt, at jeg også kunne gøre det på den måde selvfølgelig - tak for svar!
- Edit, jeg svarede dig lige inden du redigerede og skrev sidste linje, ups! Men ja, jeg fortrækker at tegne grafen hehe
Svar #9
17. juni 2021 af StoreNord
 Det der med lodret, det er vist en fejl.
Det der med lodret, det er vist en fejl.
Svar #10
17. juni 2021 af 1234vedikke
#9 kan du forklare mig hvorfor det er en fejl, funktionen fortæller blot boldens højde over tid i luften - lodret?
Det er noget med at en graf for et andengradspolynomie er symmetrisk omkring toppunktet/bundpunktet. Rent fysisk giver det sikkert ikke mening, da tyngdekraften påvirker bolden både på vej op og på vej ned
Svar #12
17. juni 2021 af Eksperimentalfysikeren
Forskriften for h er et andengradspolynomium, hvor koefficienten til andengradsleddet er negativ. Heraf følger, at det fundne ekstremum er et maksimum.
En lille sproglig bemærkning:
Ord som ekstremum, minimum, maksimum og datum er latin og hedder i flertam henholdsvis ekstrema, minima, maksima og data.
Normalt regner jeg med, at rettelser af sproget hører ind under dansk, men jeg tror ikke, at dansklæreren ser noget til disse ord, de hørrer ind under matematisk fagsprog.
Svar #13
17. juni 2021 af 1234vedikke
#12 Tak, det er altid godt at blive rettet for sproglige fejl uanset fag - det skal jeg nok huske til næste gang!
Skriv et svar til: Bestem boldens maksimale højde
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



