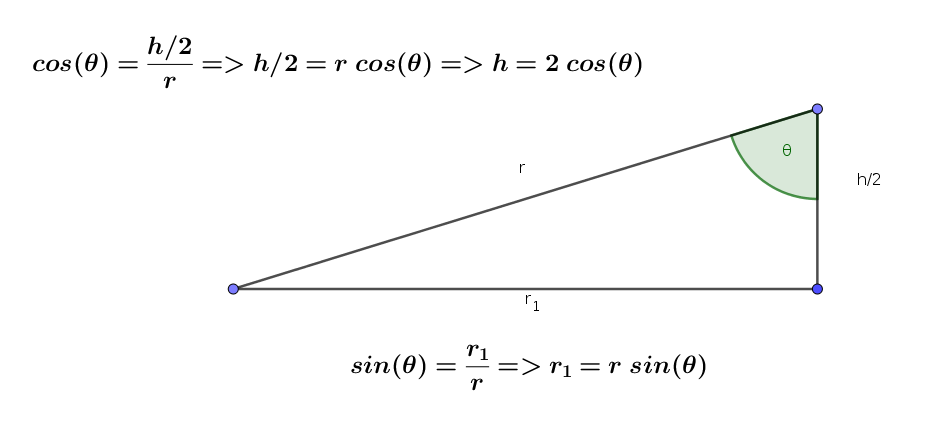Matematik
Cylinders rumfang, Vejen til Matematik B2, Opgave 148, Side 161, (Knud Erik Nielsen og Esper Fogh)
Jeg kan se at det er en opgave, der er blevet stillet tidligere, og som er besvaret af mathon, men jeg har nogle spørgsmål til nogle mellemregninger.
En cylinder er indskrevet i en kugle med radius 3 , Hvilken højde h skal cylinderen have for at dens rumfang bliver størst muligt.
Jeg har tegnet kuglen med en passer, og i kuglen har jeg tegnet et plant, lodret tværsnit gennem kuglens centrum og dernæst indtegnet et rektangel i kuglens cirkel.
Dernæst er indtegnet radius fra cirklens centrum til rektanglets øverste side den halve cylinderhøjde, h/2
Vinlen mellem (h/2) og radius r i cirklen kaldes θ
Som du skriver har man nu:
(h/2) = r* cos(θ)
h = 2*r*cos(θ)
r1 = r*sin(θ) r1 er cylinderens radius
så skulle sin(θ) = r1 / r
men ser jeg på tegningen så er r1 hypotenusen og
r er den hosliggende katete og i følge
definitionen er sin A = den modstående katete / hypotenusen
så sin A = a/c
hvoraf
V = r*sin(θ)*r12 V er cylinderens volume
Som ved indsættelse giver
V = (2r*cos(θ))*π*(r2*sin2(θ))
V = 2πr3(cos(θ) - cos3(θ)) har du gjort følgende cos2(θ) + sin2(θ) = 1
sin2(θ) = 1 - cos2(θ)
således at cos(θ) * sin2(θ) = cos(θ) (1- cos2(θ))
= cos(θ) - cos3(θ)
V = 54πr3 * (cos(θ) - cos3 (θ)) som differentieres
V' = 54π (-sin(θ) - 3cos2(θ) * (-sin(θ)) Hvordan får du (cos3)' til at blive til -3cos2(θ) * (-sin(θ))
V' = 54π (3(1-sin2(θ)) * sin(θ) - sin(θ))
V' = 54π *sin(θ) * [2 - 3sin2(θ)] = 0 hvoraf maksimum vinklen beregnes
ved brug af nul-reglen for 0 < θ < (π/2)
i hvilket interval sin(θ) > 0
hvoraf kun 2 - 3sin2((θ) = 0
-3sin2(θ) = -2
sin2(θ) = 2/3
h = 2 *r * cos(θ) = 2*3*√(1 -sin2(θ) = 2 * 3 * √(1 - (2/3)) = 2√(3)
Er cos(θ) = (1 - sin2(θ) ) regnet ud på følgende måde
cos2(θ) + sin2(θ) = 1
cos2(θ) = 1 - sin2(θ)
√cos2(θ) = √(1 - sin2(θ) )
cos(θ) = √(1- sin2(θ)) som så er indsat i ovenstående ligning
så man altså får
h = 2 * 3 cos(θ) = 2 * 3 *√(1 - sin(θ)) = 2 * 3 √(1 - (2/3)) = 2√(3)
Uden brug af f.eks TI - 89 Titanium eller et matematikprogram, hvordan regneteknisk omformer man
2 * 3 *√(1 - (/3)) til 2√3
På forhånd tak
Svar #1
02. juli 2021 af Eksperimentalfysikeren
Du undrer dig over, hvordan r og r1 opfører sig. Det kan ikke ses af det, du har vist os. Kan du ikke skanne din tegning ind?
Svar #2
02. juli 2021 af Soeffi
#0...omskriv: 2·3·√(1 - (2/3)) til 2√3
2·3·√(1 - 2/3) = 2·3·√(1/3) = 2·31·3-1/2 = 2·31-1/2 = 2·31/2 = 2√3.
Svar #4
02. juli 2021 af StoreNord
Korrektion:
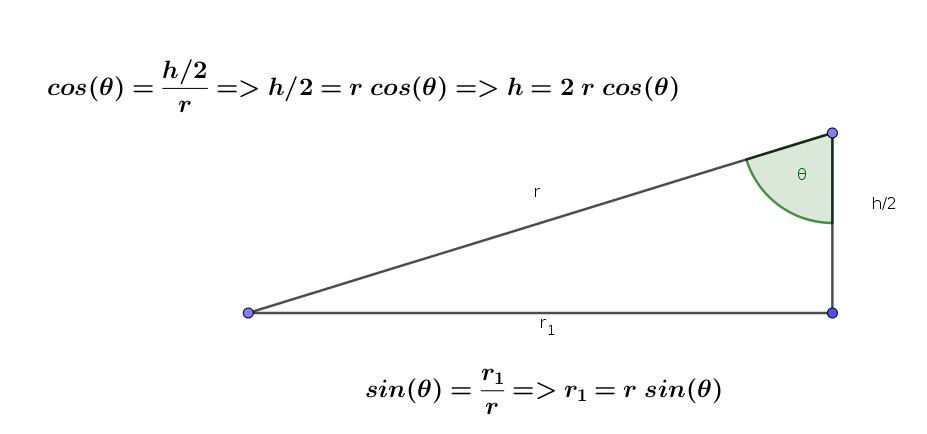
Skriv et svar til: Cylinders rumfang, Vejen til Matematik B2, Opgave 148, Side 161, (Knud Erik Nielsen og Esper Fogh)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.