Matematik

Normalvektor med længden 1 ud fra en ligning

15. august 2021 af AliceiEventyrland (Slettet) - Niveau: B-niveau

Hej SP

Hvordan finder jeg en normalvektor med længde 1, når jeg har en ligning, der siger 6x+8y+1=0?

Brugbart svar (1)

Svar #1
15. august 2021 af Eksperimentalfysikeren

Den vektor, hvis koordinater er koefficienterne til x og y, er normalvektor. Hvis du vælger 2 forskellige punkter på linien, kan du se, at dens skalarprodukt med den nævnte vektor er 0.

Brugbart svar (1)

Svar #2
15. august 2021 af mathon

$\small \small \small \begin{array}{llllll} \textup{En normalvektor er:}&\overrightarrow{n}=\begin{pmatrix} 6\\8 \end{pmatrix}\quad \left | \overrightarrow{n} \right |=\sqrt{6^2+8^2}=\sqrt{10^2}=10\\\\ \textup{En enhedsnormalvektor er:}&\overrightarrow{n}_e=\frac{1}{10 }\cdot\overrightarrow{n}=\frac{1}{10 }\cdot\begin{pmatrix} 6\\8 \end{pmatrix}=\begin{pmatrix} 0.6\\ 0.8 \end{pmatrix} \end{array}$

Brugbart svar (1)

Svar #3
15. august 2021 af ringstedLC

$\begin{align*} \textup{Linje}:a\,x+b\,y+c &= 0 \\ \vec{\,n}=\binom{a}{b}\Rightarrow \left |\!\vec{\,n}\right | &= \sqrt{a^2+b^2} \\ \left |\!\vec{\,e}_n\right | &= 1 \\ \vec{\,e}_n &= \frac{1}{\left |\!\vec{\,n} \right |}\cdot \vec{\,n}=\frac{\vec{\,n}}{\left |\!\vec{\,n} \right |}\qquad \textup{formel (44)} \\ &= \frac{1}{\sqrt{a^2+b^2}}\cdot \binom{a}{b} \\ \vec{\,e}_n &= \begin{pmatrix}\frac{a}{\sqrt{a^2+b^2}} \\\frac{b}{\sqrt{a^2+b^2}}\end{pmatrix} \\ \\ \Rightarrow \left |\!\vec{\,e}_n\right | &= \sqrt{\left (\tfrac{a}{\sqrt{a^2+\,b^2}}\right )^2+\left (\tfrac{b}{\sqrt{a^2+\,b^2}}\right )^2} \\ &= \sqrt{\tfrac{a^2+\,b^2}{a^2+\,b^2}} \\ \left |\!\vec{\,e}_n\right | &= 1 \end{align*}$

Svar #4
22. august 2021 af AliceiEventyrland (Slettet)

#3
$\begin{align*} \textup{Linje}:a\,x+b\,y+c &= 0 \\ \vec{\,n}=\binom{a}{b}\Rightarrow \left |\!\vec{\,n}\right | &= \sqrt{a^2+b^2} \\ \left |\!\vec{\,e}_n\right | &= 1 \\ \vec{\,e}_n &= \frac{1}{\left |\!\vec{\,n} \right |}\cdot \vec{\,n}=\frac{\vec{\,n}}{\left |\!\vec{\,n} \right |}\qquad \textup{formel (44)} \\ &= \frac{1}{\sqrt{a^2+b^2}}\cdot \binom{a}{b} \\ \vec{\,e}_n &= \begin{pmatrix}\frac{a}{\sqrt{a^2+b^2}} \\\frac{b}{\sqrt{a^2+b^2}}\end{pmatrix} \\ \\ \Rightarrow \left |\!\vec{\,e}_n\right | &= \sqrt{\left (\tfrac{a}{\sqrt{a^2+\,b^2}}\right )^2+\left (\tfrac{b}{\sqrt{a^2+\,b^2}}\right )^2} \\ &= \sqrt{\tfrac{a^2+\,b^2}{a^2+\,b^2}} \\ \left |\!\vec{\,e}_n\right | &= 1 \end{align*}$

Hvorfor finder man længden af normalvektoren?

Brugbart svar (0)

Svar #5
22. august 2021 af ringstedLC

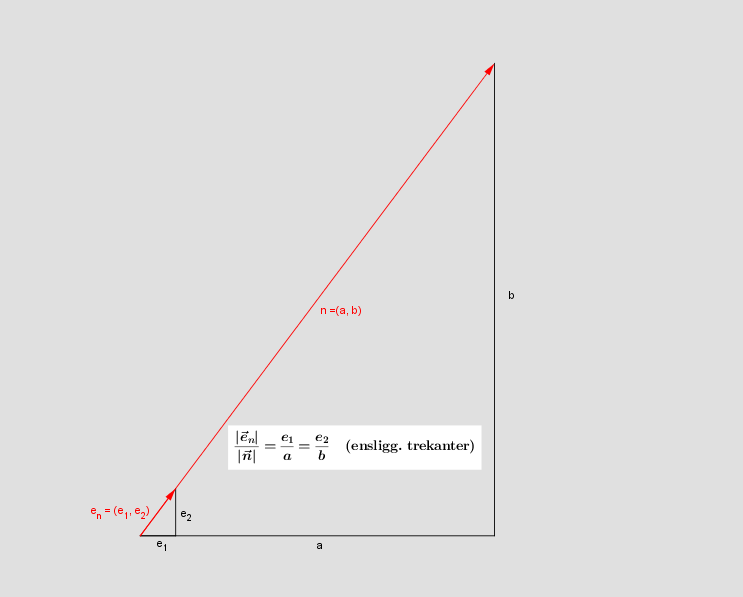
#4: Forholdet mellem længderne af vektorerne er lig forholdet mellem deres respektive koordinater:

$\begin{align*} \frac{\left |\vec{\,e}_{\!\vec{\,n}}\right |\,}{\left|\!\vec{\,n}\right |}=\frac{e_1}{a}&=\frac{e_2}{b} \\ \frac{1}{\left|\!\vec{\,n}\right|}=\frac{e_1}{a} &\Rightarrow e_1=\frac{a}{\left|\!\vec{\,n}\right |}=\frac{1}{\sqrt{a^2+b^2}}\cdot a \\ \frac{1}{\left|\!\vec{\,n}\right|}=\frac{e_2}{b} &\Rightarrow e_2=\frac{b}{\left|\!\vec{\,n}\right |}=\frac{1}{\sqrt{a^2+b^2}}\cdot b \\ \vec{\,e}_{\!\vec{\,n}}=\binom{e_1}{e_2} &= \begin{pmatrix}\frac{1}{\sqrt{a^2+b^2}}\cdot a \\ \frac{1}{\sqrt{a^2+b^2}}\cdot b\end{pmatrix}=\frac{1}{\sqrt{a^2+b^2}}\cdot \binom{a}{b} \\ &= \frac{1}{\sqrt{a^2+b^2}}\cdot \vec{\,n} \\ \vec{\,e}_{\!\vec{\,n}} &= \frac{1}{\left|\!\vec{\,n}\right|} \cdot \vec{\,n}\Rightarrow \vec{\,n}=\vec{\,e}_{\!\vec{\,n}}\cdot \left|\!\vec{\,n}\right| \end{align*}$

Vedhæftet fil:_0.png

Skriv et svar til: Normalvektor med længden 1 ud fra en ligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.