Matematik
Differentiel regning - bestem højden
Jeg har lidt problemer med opgave c her. Jeg skal bestemme højden (på det tidspunkt hvor punktet er 0). Når jeg regner på denne måde får jeg dog x værdien i stedet for y værdien (som er den værdi man kan se på billedet). Så hvordan finder jeg faktisk den rigtige værdi, det skal vises med en udregning.
Svar #1
27. september 2021 af MountAthos
Opgave c
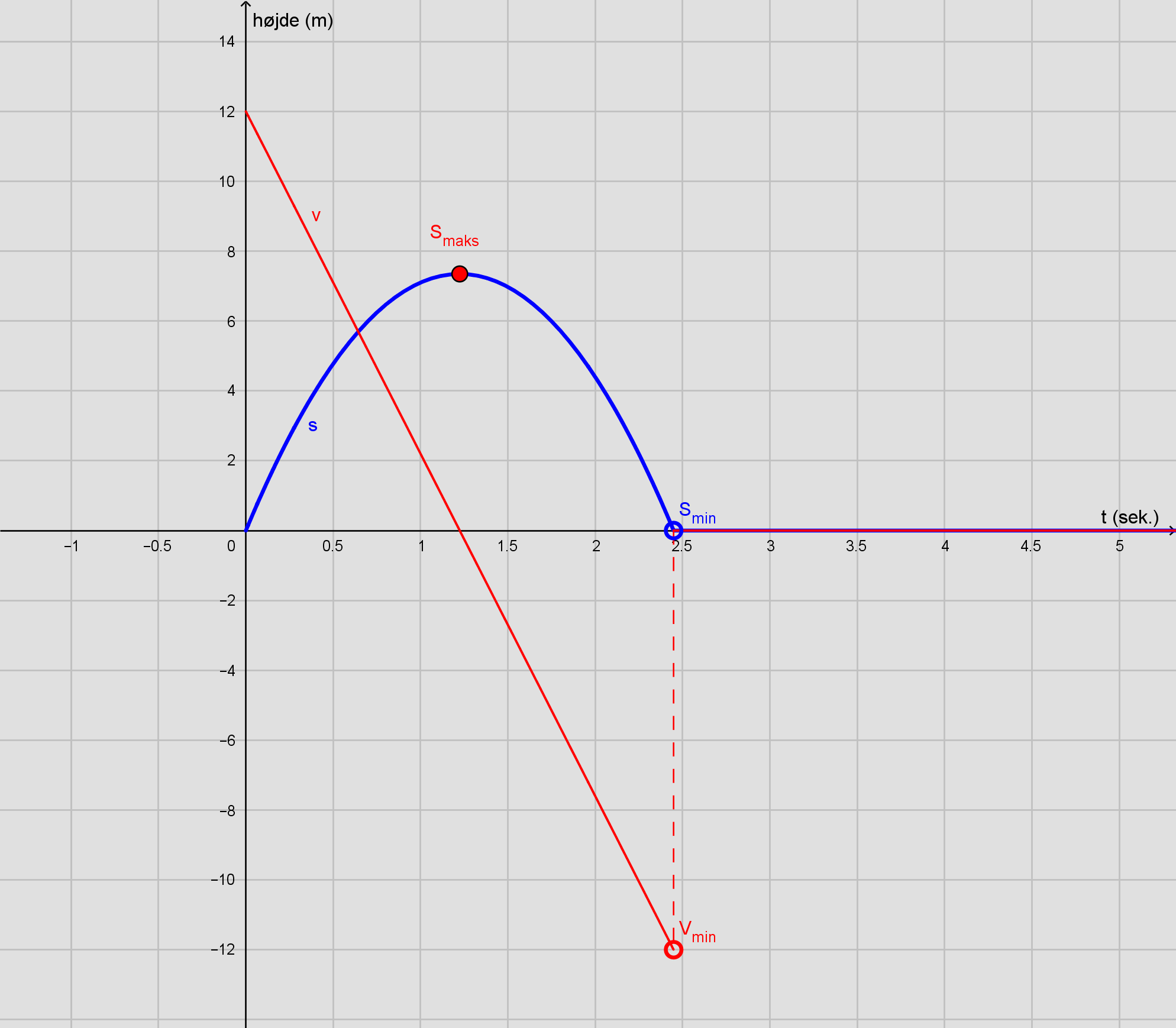
Du skal indsætte din t værdi 1,22 i s(t) = 12 · t - 4,9 · t2 , så har du højden
Skriv et svar til: Differentiel regning - bestem højden
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.