funktioner

Hej, 

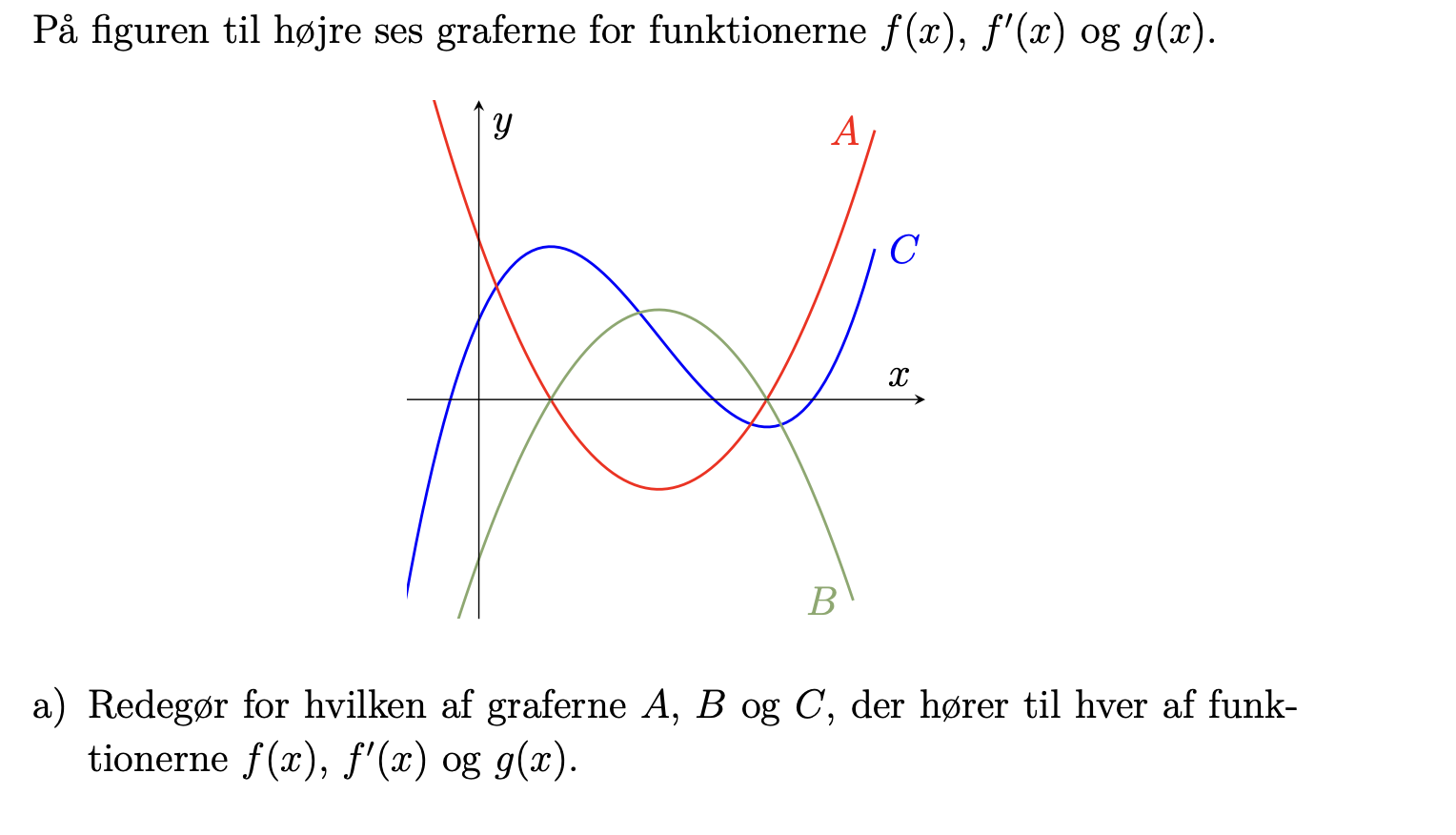
Graf C angiver et trejdegradspolynomium. Den afledede funktion til et trejdegradspolynomium er et andengradspolynomium, da man afleder 3. gradsleddet ved at gange eksponenten ned foran, og trække en fra den oprindelige eksponent. 

Da f ' er en funktion, der angiver hældningen på tangenten til et hvert punkt på grafen for f, så ved vi, at grafen for f har vandrette tangenter for f '(x) = 0. Dvs., at f har vandrette tangenter i de punkter, hvor den afledede funktion skærer x-aksen. På vores figur opfylder både graf A og B det. 

Vi kigger nu på hældningsforløbet/monotoniforholdende for grafen for f. Her kan vi se, at grafen er voksende, aftagende og voksende. Altså er fortegnet for f ' positiv, negativ og postitiv. Dette passer på graf A, mens det ikke passer på graf B.

Altså har vi redegjort for, at f(x) er angivet ved graf C, f '(x) er angivet ved graf A og g(x) er angivet ved graf B.