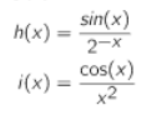Matematik

Afledte funktion

21. januar 2023 af cecilie1606 - Niveau: A-niveau

Hej

Hvordan finder jeg den afledede funktion af disse to funktioner?

Vedhæftet fil: Opgave.png

Brugbart svar (0)

Svar #1
21. januar 2023 af peter lind

Brugbart svar (0)

Svar #2
21. januar 2023 af peter lind

Du kan enten bruge formlen for en brøk f(x) = g(x)/h(x) f'(x) = (g'(x)*h(x)-g(x)*h'(x))/h(x)²

eller 1/2^-x til 2^x og tilsvarende for i(x) kan du omskrive nævneren og derefter bruge reglen om differentiation af et produkt

Svar #3
21. januar 2023 af cecilie1606

Hmm okay. Jeg er stadig ikke helt med.

Hvis nu jeg tager udgangspunkt i funktionen h(x), så siger du jeg først kan omskrive nævneren, men er stadig ikke helt med på hvad jeg helt præcis skal gøre.

Brugbart svar (0)

Svar #4
21. januar 2023 af ringstedLC

Enten:

$\begin{align*} & h(x) &&= \frac{\sin(x)}{2^{-x}} &&= \frac{f(x)}{g(x)} \\ \textup{Sammensat fkt.: } & g(x) &&= g_1\bigl(g_2(x)\bigr) \\ & g'(x) &&= \Bigl(g_1\bigl(g_2(x)\bigr)\!\Bigr)' &&= {g_1}'\bigl(g_2(x)\bigr)\cdot {g_2}'(x) \\ & g'(x) &&= \bigl(2^{-x}\bigr)' &&= \bigl(...\bigr) \\ \\ \textup{Kvotientreglen: }& h'(x) &&= \left ( \frac{f(x)}{g(x)} \right )' &&= \frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g(x)^2} \\ & h'(x) &&= \left (\frac{\sin(x)}{2^{-x}} \right )' &&= \bigl(...\bigr) \end{align*}$

Brugbart svar (0)

Svar #5
21. januar 2023 af ringstedLC

eller (til #3):

$\begin{align*} & h(x) &&= \frac{f(x)}{g(x)} &&= f(x)\cdot g(x)^{-1} \\ & h(x) &&= \frac{\sin(x)}{2^{-x}} &&= \sin(x)\cdot \bigl(2^{-x}\bigr)^{-1} &&= \sin(x)\cdot 2^{x} \\ \textup{Produktreglen: }& h'(x) &&= \bigl(f(x) \cdot g(x)\bigr)' &&= f'(x)\cdot g(x)+f(x)\cdot g'(x) \\ & h'(x) &&= \bigl(\sin(x) \cdot 2^{x}\bigr)' &&= \bigl(...\bigr) \end{align*}$

Svar #6
21. januar 2023 af cecilie1606

Okay

Er dette her rigtigt forstået?

Vedhæftet fil:Opgave 1.png

Brugbart svar (0)

Svar #7
21. januar 2023 af ringstedLC

Ja, men:

$\begin{align*} h'(x) &= \cos(x)\cdot 2^x+\sin(x)\cdot 2^x\cdot {\color{Red} \ln}(2) &,\;\textup{og ikke }In \\ &\ln(\square )\,\textup{findes sikkert i "skabeloner"} \end{align*}$

og reducér.

Svar #8
21. januar 2023 af cecilie1606

Okay super! Det er rettet.

Tak for hjælpen :)

Ift. funktionen i(x), der kan jeg vel følge samme princip.

Jeg har blot lige et spørgsmål:

Npr jeg i starten vil omregne funktionen fra brøker så jeg kan anvende produktreglen, så kommer den vel til at hedde:

i(x) = cos(x)/x^2 = cos(x)*(x^2)^-1

Men bliver det så til cos(x)*x^1 = cos(x)*x ?

Brugbart svar (0)

Svar #9
21. januar 2023 af ringstedLC

Nej:

$\begin{align*} \frac{1}{x^2} &\;{\color{Red} \neq }\;x\;,\;x\neq 1 \\ \bigl(a^r\bigr)^s &=a^{r\,\cdot\,s} \\ \bigl(x^2\bigr)^{-1} &=x^{2\,\cdot\,(-1)}=x^{\,...} \end{align*}$

Brugbart svar (0)

Svar #10
21. januar 2023 af ringstedLC

Til i(x) ville jeg bruge kvotientreglen, da:

$\begin{align*} \left (\frac{\cos(x)}{x^2}\right )' &= \frac{\bigl(\cos(x)\bigr)'\cdot x^2-\cos(x)\cdot \bigl(x^2\bigr)'}{\bigl(x^2\bigr)^2} &= - \frac{\sin(x)\cdot x+2\cos(x)}{x^3} \\\Bigl(\cos(x)\cdot x^{-2}\Bigr)' &= -\sin(x)\cdot x^{-2}+\cos(x)\cdot (-2)\cdot x^{-3} \\ &= \frac{-\sin(x)\cdot x^{-2}\cdot x^4-\cos(x)\cdot 2\cdot x^{-3}\cdot x^4}{x^4} \\ &= \frac{-\sin(x)\cdot x^{-2\,+\,4}-\cos(x)\cdot 2\cdot x^{-3\,+\,4}}{x^4} \\ \Bigl(\cos(x)\cdot x^{-2}\Bigr)' &= \frac{-\sin(x)\cdot x^2-\cos(x)\cdot 2x}{\bigl(x^2\bigr)^2} &= - \frac{\sin(x)\cdot x+2\cos(x)}{x^3} \end{align*}$

Skriv et svar til: Afledte funktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.