Matematik

Areal ved bestemt integral.

15. september 2023 af laurahansen4343 - Niveau: A-niveau

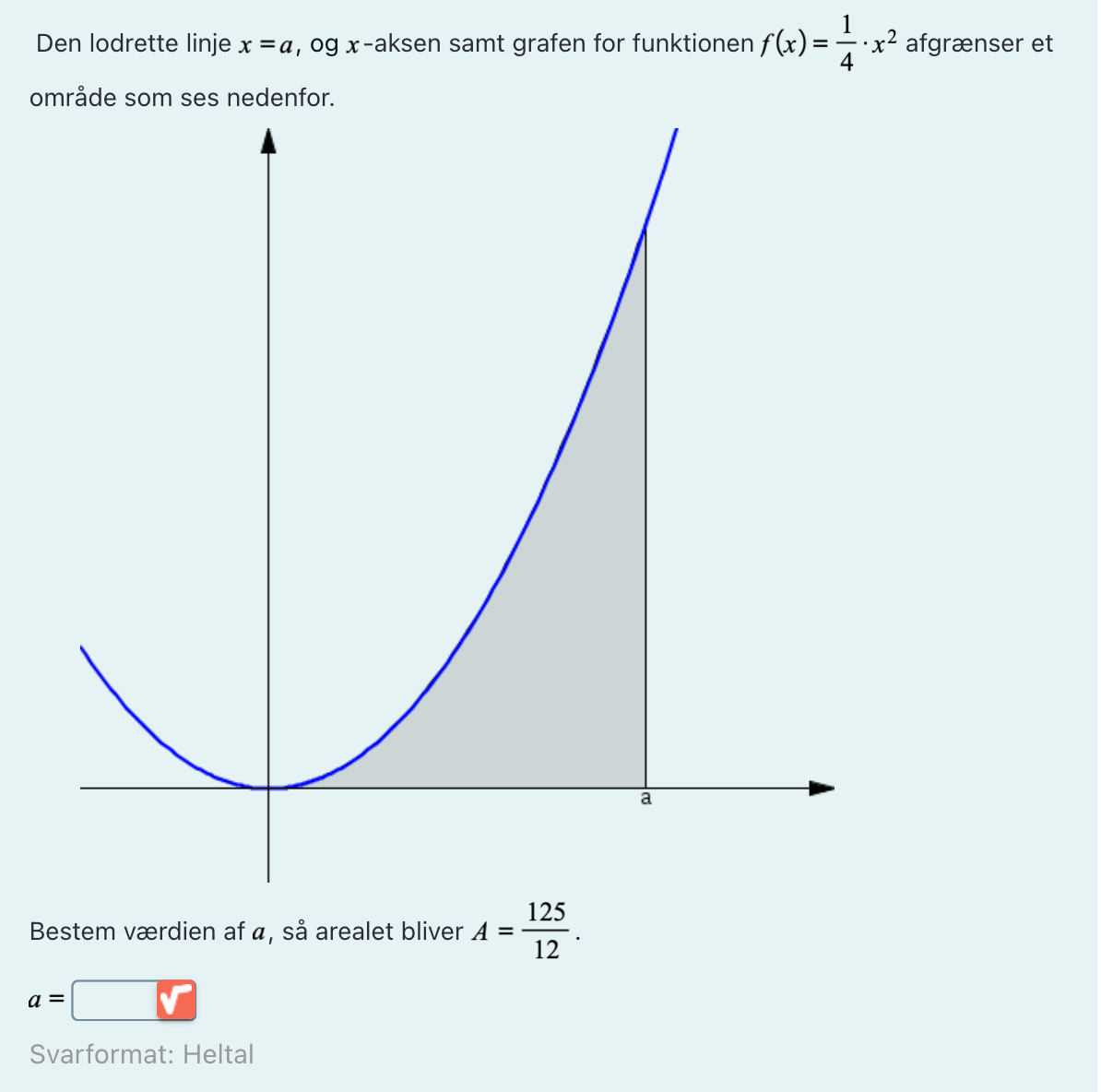
Er der en der kan hjælpe mig med at løse/forstå denne opgave, da jeg ikke forstår, hvordan jeg skal beregne arealet ud, når jeg ikke har nogle tal på x-aksen eller y-aksen??

På forhånd tak!!

Vedhæftet fil: Skærmbillede 2023-09-15 kl. 10.01.49.png

Brugbart svar (0)

Svar #1
15. september 2023 af mathon

Brugbart svar (0)

Svar #2
15. september 2023 af mathon

For en funktion
$\small f(x)\geq 0\; \forall x$
gælder
Arealet under grafen begrænset af x-aksen og de rette linjer x = a og x = b og a < b

$\small A=\int_{a}^{b}f(x)\,\mathrm(d)x$

Brugbart svar (0)

Svar #3
15. september 2023 af mathon

I anvendelse:

$\small \begin{array}{llllll}&& A=\int_{0}^{a}\frac{1}{4}x^2\,\mathrm{d}x=\frac{125}{12}\\\\ && \left [ \frac{1}{12}x^3 \right ]_0^a=\frac{125}{12}\\\\&& \frac{1}{12}\cdot a^3 -\frac{1}{12}\cdot 0^3=\frac{125}{12}\\\\&& \frac{1}{12}\cdot a^3=\frac{125}{12}\\\\&& a^3=\frac{125}{12}\cdot 12=125\\\\&& a^3=5^3\\\\&& a=\sqrt[3]{5^3}=5 \end{array}$

Svar #4
15. september 2023 af laurahansen4343

NÅrhhhh nu forstår jeg det. MAnge tak for hjælpen!

Skriv et svar til: Areal ved bestemt integral.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.