Matematik
Side 2 - sandsynligheds regning
Svar #21
10. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
hm.. det virker stadig ikke rigtigt og jeg får også 0.2
Svar #22
10. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
Jeg har tre tal "666"
sandsynlgheden for at de optræder i en streng af længde 1000 må vel være en binomial fordeling
med succesrate = 1/10^3
binom(antal gange det optræder=1,antal parameter=1000,sandsynligheds parameter=1/10^3)
Hvad er sandsynligheden for at det optræder 2 gange?
Hvad er sandsynligheden for at tre ens cifre optræder i strengen? Altså fx '111' eller fx '000' ?
Svar #23
12. september 2014 af Soeffi
Ad #20-21
1/e er grænseværdien for
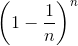
for n gående mod uendelig. Det går for vidt at bevise det.
Hvis du har en bernouilli proces, hvor p ~ 1/n og n >> k, som i denne opgave, får man approximationen:
P(antal successer = k) =

Dvs. sandsynligheden for netop to gange at finde strengen '666' er ca. 1/(2!·e) = 0,18
Svar #24
12. september 2014 af Therk
#23Dvs. sandsynligheden for netop to gange at finde strengen '666' er ca. 1/(2!·e) = 0,18
Har du taget højde for at udfaldende ikke er uafhængige og mængderne er ikke disjunkte. Tag et tilfældigt sted i strengen ved eksemplet:
...5146666913...
- optræder strengen "666" her to gange eller en gang?
...5146666913...
...5146666913...
Og i så fald hvad så med tilfældet
...852666666411...
Jeg er uenig i at det blot er en bernoulliproces. Med bernoulliprocessen i #19 fratager du også muligheden for at kunne opdage fremkomsten ved ciffer 2,3 og 4:
1666258...
bliver ikke talt med i din proces. Og da fremkomsterne ikke er disjunkte er det øjensynligt ikke så simpelt. Fremgangsmåden kunne måske være at skabe en rekursiv funktion, men hvordan et resultat eksplicit skal opskrives kan jeg ikke umiddelbart se.
Svar #25
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
#23 Hvordan får du det sidste udsagn/påstand?
Svar #26
13. september 2014 af Therk
#25#23 Hvordan får du det sidste udsagn/påstand?
http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc331.htm
Bernoullifordelingen er binomialfordelingen med n = 1.
Svar #27
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
Men du skal stadig redegøre for
n!/(n-k)! =1
(1/n)^k * (1-1/n)^(-k) = 1
for n stor
Svar #28
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
Udtrykket giver simpelthen ingen mening.
1/(k!e) er uafhæng. af strengens længde. Antallet af succeser k indgår men længden fx 1000 indgår ikke.
Svar #29
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
jo, nu har jeg selv udledt det. Men det er stadig mærkeligt at det ikke afhænger af strengens længde
Svar #30
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
glem hvad jeg har skrevet - jeg har forstået det nu.
Det vækker et andet filosofisk spørgsmål: For et tilfældig tal vil der dermed indgå mærkelige sekvenser.
Fx vil der være 10^100 nuller efter hinanden i tallet e=2.71.......
Jamen så ved vi at sandsygheden for dette er
P(antal succeser <=0)=1 - P(antal succer =0)
=1 - 1/(0!*e) =1-1/e
Er det ikke rigtigt forstået ?
Svar #31
13. september 2014 af Soeffi
Ad #24
Det er rigtigt, men siden det ikke er præciseret i opgaven, går jeg ud fra, at det ikke gør den store forskel.
Ad #25
Det kaldes Poissons grænse teorem for p·n ca lig 1
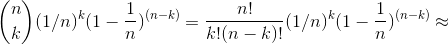
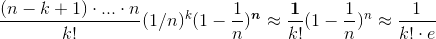
Svar #32
13. september 2014 af Therk
#31Ad #24
Det er rigtigt, men siden det ikke er præciseret i opgaven, går jeg ud fra, at det ikke gør den store forskel.
Det gør da en kæmpe forskel - den største forskel består i at de udregnede approksimationer slet ingen basis har. Jeg vil gå så langt som at sige det er sammenligneligt med at estimere differentialkvotienten for 1/x i x=0 vha. et tilfældigt andengradspolynomium.
Svar #33
13. september 2014 af Soeffi
Så må det jo præciseres i opgaven, hvad der menes, ellers kan den jo ikke løses.
Svar #34
13. september 2014 af thomaslarsen90Arocketmailcom (Slettet)
#33 Hans approksimation fejler da ikke noget?
Skriv et svar til: sandsynligheds regning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








