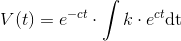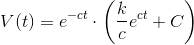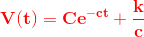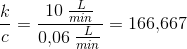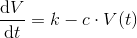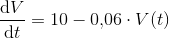Matematik
Differentialligning om badekar model
Hej.
Jeg skal opstille en differentialligning til en model om et badekar, hvor der er en konstant som addere vand til rumfanget af badekarret, men også en funktion der afhænger af hvor meget vand der er i badekarret, som lukker vandet ud igen.
I opgaven står der at jeg skal finde en passende differentialligning til denne model, men aner virkelig ikke hvordan jeg skal gribe det an.
Opgaven og modellen er vedhæftet som en fil.
Svar #1
21. juli 2016 af Moderatoren
Du kan desværre ikke vedhæfter filer pt.
Du skal i stedet selv skrive opgaveformuleringen ind.
Svar #2
21. juli 2016 af Mallingg (Slettet)
Formlen for badekarret ser sådan her ud:
Vi får oplyst at:
Indstrømningskonstanten for vand fra hanen:
10 L
k = ----
min
Udstrømningskonstanten er propotional med bandoverfladens højde over bunden. Hvilket vil sige at udstrømningstrykket stiger propotionalt med mængden af vand i badekaret.
0.06
c = ----
min
Badekarrets totale rumfang er 250L
V := 250 L
Mens rumfanget af vand som funktion af tiden:
V(t)
, startværdi
V(0) = 0
Derfor er formlen:
V(t+delta(t))=V(t)+k*delta(t) - c*V(t)*delta(t)
Jeg skal finde en differentialligning for denne model som passer ind.
Vores lærer siger at det ikke er logistisk vækst, og nogen fra klassen mener at det er en kombination af flere differentialligninger
Håber det er forståeligt
Malling
Svar #3
21. juli 2016 af Mallingg (Slettet)
Jeg har forsøgt mig lidt frem og er kommet til noget lignende dette:
V'(t)=k-c*V(t)
Ved ikke om jeg skal skal skrive k(t), da mængden jo bliver større, jo mere tid der går.
Svar #4
21. juli 2016 af Eksperimentalfysikeren
Du er næsten fremme ved differentialligningen. Start med at trække V(t) fra på begge sider af lighedstegnet. Divider så ligningen igennem med delta(t). V(t+delta(t))-V(t) skriver du som delta(V) Så har du differensligningen, som du omskriver til differentialligning ved at erstatte delta(t) med dt og delta(V) med dV.
Normalt skriver man ikke delta(t), men Δt, men jeg fornemmelsen af, at du ikke har den mulighed til rådighed.
Svar #5
21. juli 2016 af Eksperimentalfysikeren
Du kom mig i forkøbet. Din ligning er korrekt. k er konstant, så du behøver ikke at skrive k(t).
Svar #6
21. juli 2016 af Mallingg (Slettet)
okay, jeg prøver :)
-Ja, jeg skriver også en trekant men ved ikke hvordan man gør i html :)
Svar #7
21. juli 2016 af Mallingg (Slettet)
Men jeg har ikke gjort det du skrev jeg skulle. Måske uden at vide det.
Jeg havde bare tænkt at det der løber ud som er propotional med mængden af vand skal trækkes fra k.
Mallingg
Svar #8
21. juli 2016 af Eksperimentalfysikeren
Δ ( & D e l t a ; )
Over indtastningsfeltet på SP's hjemmeside er det et Ω. Klikker man på det, kommer der en del forskellige tegn frem, heriblandt Δ.
Svar #9
21. juli 2016 af Mallingg (Slettet)
Altså jeg bruger maple hvor jeg angiver det som symboler :)
Svar #10
21. juli 2016 af Eksperimentalfysikeren
Hvis din metode har været at sige: Ændringshastigheden for vandmængden = tilført vandmængde - udløbende vandmængde, så har du i virkeligheden sagt det samme som den oprindelige ligning og omregningen er det, jeg har omtalt.
Svar #12
21. juli 2016 af Mallingg (Slettet)
Okay, nu skal jeg bare have den til at ligne differentialligning 2: y'+ay=b
Jeg går ud fra at i min ligning: V'(t)=k-c*V(t) er:
V'(t)=y'
k=b
c=a
V(t) =y
er dette korrekt? så skal jeg bare have omskrevet den igen, så det står på den rigtige side ikk?
Mallingg
Svar #15
21. juli 2016 af Mallingg (Slettet)
Okay, ja det var sådan der jeg havde tænkt det mathon.
Jeg var faktisk i tvivl om man godt måtte addere 2 led med gangetegn imellem på begge sider af lighedstegnet. (der hvor du rykker -c*V(t) over på venstre side.)
Mange tak for hjælpen alle :)
Mallingg
Svar #16
21. juli 2016 af Mallingg (Slettet)
Mathon hvorfor dividere du k med c i panserformlen. k bliver sat udenfor integralet.
Jeg er bare lidt i tvivl hvordan jeg forklarer k/c?
Mallingg
Svar #18
22. juli 2016 af Mallingg (Slettet)
okay, jeg kan se at jeg skal bruge 3 trinsreglen for at finde differenskvotienten, men det mener jeg allerede er gjort da jeg fandt differentialligningen.
Der hvor vi lader den gå mod 0.
Mallingg
Skriv et svar til: Differentialligning om badekar model
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








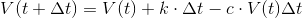
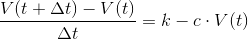 som for
som for 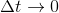
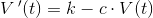
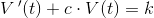 som ved brug af panserformlen
som ved brug af panserformlen