Matematik
Analyse 2
Nogen der kan forklare mig eksemplet i bogen?
De lige tal er tællelige. Det følger af
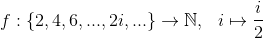
er en injektion og endda også en bijektion. Det betyder at der er lige så mange naturlige tal som der er naturlige tal....
-----------
Der er tale om en injektion for ifølge definitionen:
Injektion: f(x) = f(x') ⇒ x = x'
er det klart...
Men da det også er en bijektion - da vil det sige at den også er surjektiv.
Surjektiv: f(X) := {f(x)∈Y : x∈X} = Y
Men det vil sige, at til ethvert element y∈Y findes mindst ét element x∈X, sådan at φ(x) = y
Men vælger vi y = 3, så kan vi altså ikke finde sådan et x som opfylder betingelsen... Eller har jeg misforstået noget?
Svar #2
24. august 2017 af swpply (Slettet)
Surjektivitet følger af at der trivielt gælder om f at
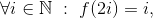
hvorfor specielt at i = 6 bliver afbiledet til 3.
Svar #3
24. august 2017 af swpply (Slettet)
Og du kan vise injektivitet ved at antage (for modstrid) at der findes i og j således at i ≠ j og f(i) = f(j).
Svar #4
24. august 2017 af Stats
Ahr... For fanden man... Det er sQ da rigtig :)
Mange tak :)
Mvh Dennis Svensson
Svar #5
24. august 2017 af Stats
(dette er ikke en opgave, men et eksempel som jeg forsøger at forstå)
Nu har jeg så et andet spørgsmål ang. et andet eksempel. De skriver at
(iii) The set of intergers
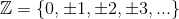
is countable. A possible counting scheme is shown on the right or, more formally (af gode grunde kan i ikke se billedet)
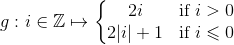
hence #Z ≤ #N
Det vil jo ikke betyde, at kardinaliteten i de hele tal generelt er mindre end kardinaliteten i de naturlige tal? Det er vel kun i dette tilfælde at det gør sig gældende?
(Undskyld hvis jeg spørg til noget man burde vide.)
Mvh Dennis Svensson
Svar #6
24. august 2017 af peter lind
Du kan aldrig slutte at kardinaliteten af de hele tal er mindre end kardinaliten af de lige tal.
I dette tilfælde er den faktisk også bijektiv. Den inverse funktktion lyder
gº-1(j) er j/2 hvis j er lige og (j-1)/2 hvis den er ulige
Svar #8
24. august 2017 af swpply (Slettet)
Jeg kan næsten gætte mig til at du bruger bogen Measures, Integrals and Martingales af Schilling.
Det vil jo ikke betyde, at kardinaliteten i de hele tal generelt er mindre end kardinaliteten i de naturlige tal? Det er vel kun i dette tilfælde at det gør sig gældende?
Husk hvad definition af kardinalitetes begrebet siger!
Hvis X og Y er to mængder, samt at der eksitere en injektik afbildning fra X til Y. Så siger vi at kardinaliteten af X er "svagt mindre end" kardilateten af Y. Hvis afbildingen ikke er surjektiv (men kun injecktiv) siger vi at kardinaliteten af X er "strengt mindre end" kardilateten af Y. Og til slut, siger vi ar kardilateten af X er "lig" kardinaliteten af Y såfremt at der eksitere en bijektiv afbilding.
Kardinalitetes begrebet udsiger sig altså blot noget om eksitensen (eller manglen der på) af en (eller flere) injektive afbildinnger imellem to mængder. Det udsiger sig altså ikke noget om hvorledes der er fære eller flere elementer i den ene mængde end den anden — for at kunne slutte nogen om dette skal du bruge udvalgs aksimonet. Hvis du ikker har støt bekendtskab med at bruge udvalgsaksioment, skal du ikke fortivle og blot udryste dig med tålmodighed til at du tager et kursus over topologi.
For at vende tilbage til dit sprøgsmål, så betyder udsagnet
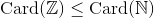
blot at der eksietere mindst en injektiv afbilding (som måske også er surjektiv ... ≤ vs. <) fra de hele tal til tælletallene. Det betyder altså ikke at der enten er mindre (eller lige mange) elementer i de hele tal som i tælletallene.
Knæk og bræk med analysen :-)
Svar #9
25. august 2017 af Stats
Hvis X og Y er to mængder, samt at der eksitere en injektik afbildning fra X til Y. Så siger vi at kardinaliteten af X er "svagt mindre end" kardilateten af Y. Hvis afbildingen ikke er surjektiv (men kun injecktiv) siger vi at kardinaliteten af X er "strengt mindre end" kardilateten af Y. Og til slut, siger vi ar kardilateten af X er "lig" kardinaliteten af Y såfremt at der eksitere en bijektiv afbilding.
Og det er også det som forvirre mig.... "#" i vores bog bliver anvendt som kardinaliteten.
1. f : X → Y ; hvis der eksistere en injektion ⇒ #X ≤ #Y
2. f : X → Y ; hvis der eksistere en bijektion ⇒ #X = #Y
3. f : X → Y ; hvis der eksistere en injektion og ikke en surjektion ⇒ #X < #Y
Men er 1 og 3 ikke stort set det samme? Eller anvender man kun 1. fordi man ikke har "gidet" eller kan tjekke for surjektiv? (Jeg kan nemlig huske, at nogen mennesker konsekvent anvender tilfældet "≤" fordi "så siger man ikke noget forkert.")
Mvh Dennis Svensson
Svar #10
25. august 2017 af swpply (Slettet)
... anvender man kun 1. fordi man ikke har "gidet" eller kan tjekke for surjektiv?
Både ja og nej.
Antag at du er givet én injektiv (men ikke surjektiv) afbilding fra X til Y ⇒ #X ≤ #Y.
(her arbejder du med en kokret afbilding)
For at du kan slutte at #X < #Y, skal du vise at der iblandt samtlige inkeltive afbildinger ikke eksitere en afbilding der også er surjektiv. Du skal med andre ord "prove a negative".
(her arbejder med samtlige afbildinger, altså ikke med nogen konret afbilding).
Men det kan også sagtnes forholde sig som du skriver, at man simpelthen ikke er intreeseret i den surjektive egensak men blot den injektive egenskab ved afbildingen. Hvorfor man vil skrive #X ≤ #Y for at indirekte undrerstrege dette overfor læseren.
Jeg kan nemlig huske, at nogen mennesker konsekvent anvender tilfældet "≤" fordi "så siger man ikke noget forkert.
Personligt, er det god "stil" i et bevis ikke at specificere mere end hvad der nødvendigt og tilstrækkeligt for bevise den ønskede påstand. Så hvis du kun skal bruge at der eksitere en injektiv afbilding f:X->Y. Vil man eksempelvis skrive #X ≤ #Y. Og tilsvarende hvis man skal bruge enten injektiv men ikke surjektiv eller bijektivitet.
Så det er ikke så meget "frygten" for at sige noget forkert. Men mere at der er ikke nogen grund til at specifiere et stærkere udsagn end hvad der er nødvendigt og tilstrækkeligt i den pågældende situation.
Skriv et svar til: Analyse 2
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





