Matematik

Talfølge går mod uendelg

12. november 2018 af Jensssssssssssss (Slettet) - Niveau: Universitet/Videregående

Hej SP

Jeg har vedhæftet et billede, hvor jeg skal vise talfølgen inde i parentensen er konvergent og herudover finde dens sum (se bort fra lim....) (der er også en lille fejl, enten skal der stå k alle steder, eller x alle steder..)

Håber der er en, der kan hjælpe

Vedhæftet fil: Skærmbillede 2018-11-12 kl. 19.39.51.png

Brugbart svar (0)

Svar #1
12. november 2018 af MatHFlærer

Det skulle vel tilfældigvis ikke være "k" og ikke "x" i dit sigma... ?

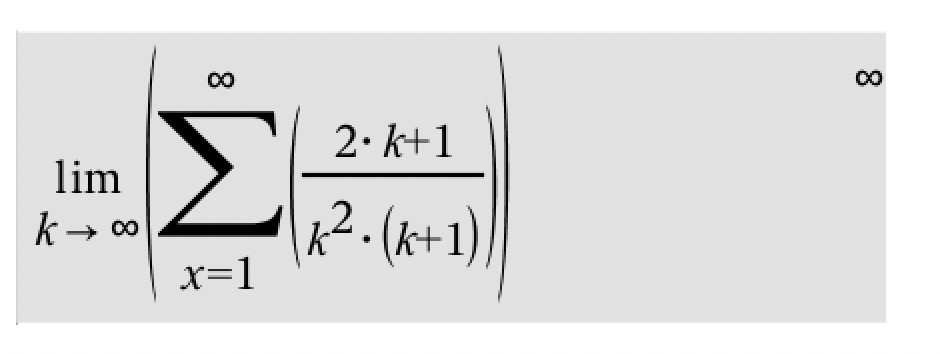
Svar #2
12. november 2018 af Jensssssssssssss (Slettet)

Som jeg nævnte, der skal stå enten k eller x alle steder :)

Svar #3
12. november 2018 af Jensssssssssssss (Slettet)

se herunder

Vedhæftet fil:Skærmbillede 2018-11-12 kl. 19.47.28.png

Brugbart svar (0)

Svar #4
12. november 2018 af peter lind

Skriv indmaden som ((k+1)+k)/(k²(k+1)) = 1/k²+1/(k(k+1)

Brugbart svar (0)

Svar #5
12. november 2018 af MatHFlærer

Ahh sorry!

Brugbart svar (0)

Svar #6
12. november 2018 af MatHFlærer

Ja, udnyt det Peter Lind skrev, dvs.

$\sum_{k=1}^\infty \frac{2k+1}{k^2(k+1)}=\sum_{k=1}^\infty \frac{1}{k^2}+\sum_{k=1}^\infty \frac{1}{k(k+1)}$

Brugbart svar (0)

Svar #7
12. november 2018 af MatHFlærer

Okay, du kan nemt afgøre om den konvergerer eller divergerer. Tænk på p-series.

$\sum _{n=1}^\infty \frac{1}{n^p}=1+\frac{1}{2^p}+\frac{1}{3^p}+\cdots$

Her er $p>0$ pr. definition. Derudover gælder

- Hvis $p>1$ , så konvergerer rækken.

- Hvis $0<p\leq 1$ så divergerer rækken.

Det er nemt at afgøre det, hvis du bruger anbefalingen fra Peter Lind.

Brugbart svar (0)

Svar #8
12. november 2018 af MatHFlærer

Men det var kun for første del af rækken. Jeg tænker telescoping series kan anvendes til næste del. NB: rækken med $1/k^2$ er kendt, som giver $\pi^2/6$ .

Vi kigger på

$\sum _{k=1}^ n \frac{1}{k^2+k}$ Bemærk, at:

$\frac{1}{k^2+k}=\frac{1}{k}-\frac{1}{k+1}$

Så

$\sum _{k=1}^ n \left(\frac{1}{k}-\frac{1}{k+1}\right)=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{n-1}-\frac{1}{n}\right)+\left(\frac{1}{n}-\frac{1}{n+1}\right)$

Dvs.

$\sum _{k=1}^ n \left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1}$

Og tager du grænseværdien af ovenstående, for $n\rightarrow \infty$ , så får du $1+0=1$ . Altså er dit svar til rækken

$\sum_{k=1}^\infty \frac{2k+1}{k^2(k+1)} =1+\frac{\pi^2}{6}$

Svar #9
12. november 2018 af Jensssssssssssss (Slettet)

Sikke et arbejde, jeg takker mange gange!

Hvordankan 1/k^2 = (pi^2)/6?

Brugbart svar (0)

Svar #10
12. november 2018 af MatHFlærer

Du kan læse om det her: https://en.wikipedia.org/wiki/Basel_problem

Svar #11
12. november 2018 af Jensssssssssssss (Slettet)

Takker endnu engang!

Svar #12
12. november 2018 af Jensssssssssssss (Slettet)

#4 hvordan kommer du frem til udtrykket?

Skriv et svar til: Talfølge går mod uendelg

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.