Matematik

En kasse

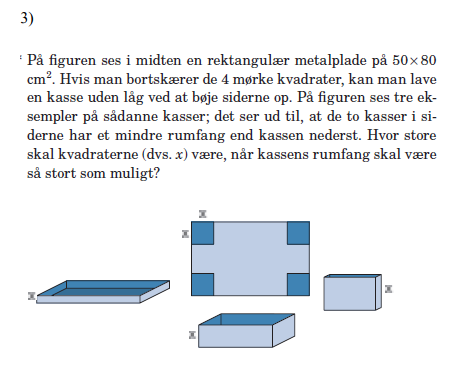
11. januar 2019 af Hanne12345654321 - Niveau: B-niveau

Hej, kan nogen hjælpe mig med denne opgave, da jeg ikke ved, hvordan jeg skal løse den? (tjek billede)

Tak på forhånd:)

Vedhæftet fil: mat.PNG

Brugbart svar (1)

Svar #1
11. januar 2019 af peter lind

Brugbart svar (1)

Svar #2
11. januar 2019 af peter lind

Kald længden af siden L og bredden for B får man at kassens bund har arealet (L-2X)(B-2x) og højden x. Rumfanget bliver derfor x(L-2X)(B-2x) Den maksimal rumfang kan findes ved at finde den aflede af rumfanget med hensyn ti x og sætte den lig 0

Svar #3
11. januar 2019 af Hanne12345654321

Ej jeg forstår det ikke:(

Brugbart svar (0)

Svar #4
11. januar 2019 af peter lind

Hvad forstår du ikke ?

Svar #5
11. januar 2019 af Hanne12345654321

Altså hele din forklaring. Kan du forklare det på en anden måde?

Brugbart svar (0)

Svar #6
11. januar 2019 af peter lind

Det er altså ikke meget hjælp jeg får til at besvare dit spørgsmål. Se på figuren, Længeden bliver fomindsket med 2x. Det samme sker for bredden. Højden bliver x. Rumfanget er længde*bredde*højde

Brugbart svar (1)

Svar #7
12. januar 2019 af ringstedLC

Opgavens oplysninger er en smule tvetydige. Det er op til dig, om du vil bruge én- eller begge af følgende løsninger.

Når du skal finde det største/mindste eller korteste/længste af et eller andet, kaldes det at optimere. Her er differentialregning et godt værktøj. Men det kræver, at du laver en funktion for det, der skal optimeres.

a) Rumfangsfunktion beregnes udfra dimensionerne L og B:

$\begin{align*} Dimensioner&= L\times B \\ & =80\cdot 50\;cm^2\;l\ae st\;som\;L=80\;cm\;,\;B=50\;cm \\ R(x) &= L\times B\times H \\ &=(80-2x)\cdot (50-2x)\cdot x\;,\;x>0\wedge x<\tfrac{50}{2} \\ &=(80-2x)\cdot (50x-2x^2) \\ &=4000x-160x^2-100x^2+4x^3 \\ &=x^3-65x^2+1000x \\ R'(x)&=3x^2-130x+1000 \\ R'(x)=0&=3x^2-130x+1000 \\ x=10&\vee x=33.33\;(forkastes) \\ Areal_{kvadrat}&=x^2=10\cdot 10\;\left ( cm\cdot cm \right )=100\;cm^2 \end{align*}$

b) Rumfangsfunktion beregnes udfra arealet af pladen. Her benyttes at pladen skal udskæres kvadratisk, så kassen bliver kubisk og derved opnår det største rumfang:

$\begin{align*} Areal_{plade}&=80\cdot 50\;cm^2\;l\ae st\;som\;4000\;cm^2 \\ R_{kube}&=\left(\sqrt{4000}-2x\right)^2\cdot x\;,\;x>0\wedge x<\tfrac{\sqrt{4000}}{2}\approx31.62 \\ &=\left(4000+4x^2-4\sqrt{4000}\cdot x\right)\cdot x \\&=x^3-\sqrt{4000}\cdot x^2+1000x \\ {R_{kube}}'(x)&=3x^2-2\sqrt{4000}\cdot x+1000 \\ {R_{kube}}'(x)=0&=3x^2-2\sqrt{4000}\cdot x+1000 \\x\approx10.54&\vee x\approx31.62\;(forkastes) \\ Areal_{kvadrat}&=x^2=10.54\cdot 10.54\;\left ( cm\cdot cm \right )=111.09\;cm^2 \end{align*}$

Til forfatteren af opgaven: I den virkelige verden har man ikke plade på "50x80 cm²". Man har en plade, der er 50 x 80 cm. Og man "bøjer ikke siderne op" på en metalkasse, de bukkes.

Skriv et svar til: En kasse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.