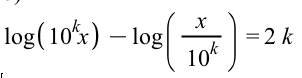Matematik

Bevise logaritmer er rigtige med grundmængderne

10. februar 2019 af careell - Niveau: B-niveau

Hej, jeg er ved det sidste i min aflevering. Jeg mangler den her opgave som jeg ellers gemte den allersidst, som så er nu. Jeg har prøvet at få det til at virke i mit hovede i et stykke tid nu, men det har ikke lykkedes.

Jeg skal få log(10^k*x)-log(x/10^k) til at give 2*k (også vedhæftet i fil)

Vil bare høre om nogle kunne hjælpe, og bevise at det giver 2*k?

Vedhæftet fil: Skærmbillede 2019-02-10 kl. 21.27.31.png

Brugbart svar (0)

Svar #1
10. februar 2019 af oppenede

$\large 2k=\log(10^{2k})=\log(10^k x/(x/10^k))=\log(10^k x)-\log(x/10^k)$

Brugbart svar (0)

Svar #2
10. februar 2019 af peter lind

Log(10^k*x)= Log(10^k)+Log(x) = k +log(x)

Ren selv tilsvarende det andet ed ud

Brugbart svar (0)

Svar #3
10. februar 2019 af Eksperimentalfysikeren

log(10^kx)-log(x/10^k) = log(10^k)+log(x)-(log(x)-log(10^k))=

k*log(10)+log(x)-(log(x)-k*log(10))=

k*1+log(x)-(log(x)-k*1))=

k+log(x)-log(x)+k=

Brugbart svar (1)

Svar #4
11. februar 2019 af AMelev

Log og 10^ er hinandens inverse - de "ophæver hinanden", så Log(10^noget) = noget

Log (10^k · x) Produktreglen
$\textup{Log}(\frac{x}{10^k})$ Brøkreglen

Skriv et svar til: Bevise logaritmer er rigtige med grundmængderne

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.