Matematik

har brug for hjælp

02. marts 2019 af Nanna34 - Niveau: B-niveau

har lavet 1 men er blank i 2.a

Vedhæftet fil: Screen Shot 2019-03-02 at 13.23.17.png

Brugbart svar (0)

Svar #1
02. marts 2019 af AMelev

Brugbart svar (0)

Svar #2
02. marts 2019 af AMelev

2a) Som der står i hintet, skal du differentiere venstresiderne i ligningerne.
Vær obs på, at begge led er produkter og cos(k·x) og sin(k·x) er sammensatte funktioner.
$(y(x)\cdot cos(k\cdot x)-\frac{1}{k}\cdot y'(x)\cdot sin(k\cdot x))'=$
$y'(x)\cdot cos(k\cdot x)-k\cdot y(x)\cdot sin(k\cdot x)- \frac{1}{k}\cdot(y''(x)\cdot sin(k\cdot x)+k\cdot y'(x)\cdot cos(k\cdot x))=$

$-k\cdot y(x)\cdot sin(k\cdot x)-\frac{1}{k}\cdot y''(x)\cdot sin(k\cdot x)=$ $-k\cdot y(x)\cdot sin(k\cdot x)-\frac{1}{k}\cdot (-k^2\cdot y(x))^{\color{Red} {*)}}\cdot sin(k\cdot x)=0$

$\color{Red}^ {*)}$ Iflg. differentialligningen.

Samme procedure for den anden ligning.

Svar #3
02. marts 2019 af Nanna34

-

Vedhæftet fil:Screen Shot 2019-03-02 at 15.11.46.png

Svar #4
02. marts 2019 af Nanna34

tak

Svar #5
02. marts 2019 af Nanna34

.

Svar #6
02. marts 2019 af Nanna34

Brugbart svar (0)

Svar #7
02. marts 2019 af AMelev

#3 Der er en fortegnsfejl i sidste led i 2. linje (-1/k) skal ganges på begge - ellers får du ikke 0, når du reducerer.
Desuden skal der parentes om -sin(kx) i 2.led i 3. linje (de skal jo ganges) og y'' skal ganges med sin(kx) udifferentieret.

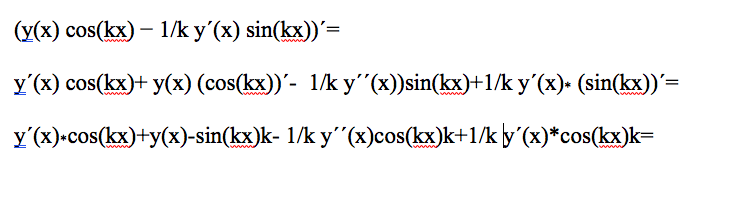
$y'(x)\cdot cos(kx)+y(x)(-sin{\color{Red} (}kx){\color{Red} )}k-\frac{1}{k}y''(x){\color{Red} sin}(kx){\color{Red} -}\frac{1}{k}y'(x)\cdot cos(kx)k$
Når du så indsætter y'' = -k²y, kan du reducere til 0

Svar #8
02. marts 2019 af Nanna34

#7 er helt blank
#3 Der er en fortegnsfejl i sidste led i 2. linje (-1/k) skal ganges på begge - ellers får du ikke 0, når du reducerer.
Desuden skal der parentes om -sin(kx) i 2.led i 3. linje (de skal jo ganges) og y'' skal ganges med sin(kx) udifferentieret.

$y'(x)\cdot cos(kx)+y(x)(-sin{\color{Red} (}kx){\color{Red} )}k-\frac{1}{k}y''(x){\color{Red} sin}(kx){\color{Red} -}\frac{1}{k}y'(x)\cdot cos(kx)k$
Når du så indsætter y'' = -k²y, kan du reducere til 0

Vedhæftet fil:Screen Shot 2019-03-02 at 19.13.09.png

Svar #9
02. marts 2019 af Nanna34

#8
#7 er helt blank
#3 Der er en fortegnsfejl i sidste led i 2. linje (-1/k) skal ganges på begge - ellers får du ikke 0, når du reducerer.
Desuden skal der parentes om -sin(kx) i 2.led i 3. linje (de skal jo ganges) og y'' skal ganges med sin(kx) udifferentieret.

$y'(x)\cdot cos(kx)+y(x)(-sin{\color{Red} (}kx){\color{Red} )}k-\frac{1}{k}y''(x){\color{Red} sin}(kx){\color{Red} -}\frac{1}{k}y'(x)\cdot cos(kx)k$
Når du så indsætter y'' = -k²y, kan du reducere til 0

fandt ud af det sku ba kigge på det lidt;)))

Brugbart svar (0)

Svar #10
02. marts 2019 af AMelev

Der kan du bare se :)

Har du styr på b) nu også? Ellers spørger du bare igen.
Du skal udnytte, at sin²(...) + cos²(...) = 1.

Svar #11
02. marts 2019 af Nanna34

#10
Der kan du bare se :)

Har du styr på b) nu også? Ellers spørger du bare igen.
Du skal udnytte, at sin²(...) + cos²(...) = 1.

det havde jeg ogs gjort va ba alt for dovn ....men takkkkk

Vedhæftet fil:Screen Shot 2019-03-02 at 19.50.16.png

Svar #12
02. marts 2019 af Nanna34

#10
Der kan du bare se :)

Har du styr på b) nu også? Ellers spørger du bare igen.
Du skal udnytte, at sin²(...) + cos²(...) = 1.

men kan du hjælpe mig med sidst opgave ogs:)

Brugbart svar (0)

Svar #13
02. marts 2019 af AMelev

$y(x)\cdot cos^2(k\cdot x)-\frac{1}{k}\cdot y'(x)\cdot sin(k\cdot x)\cdot cos(k\cdot x)=c_1\cdot cos(k\cdot x)$
$y(x)\cdot sin^2(k\cdot x)-\frac{1}{k}\cdot y'(x)\cdot cos(k\cdot x)\cdot sin(k\cdot x)=c_2\cdot sin(k\cdot x)$

Læg dem sammen og sæt y(x) uden for parentes på venstre side og udnyt "fidusen" fra # 10.
Upload det, du får, hvis du ikke kan komme helt hjem, så du kan hjælpes videre.

Skriv et svar til: har brug for hjælp

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.