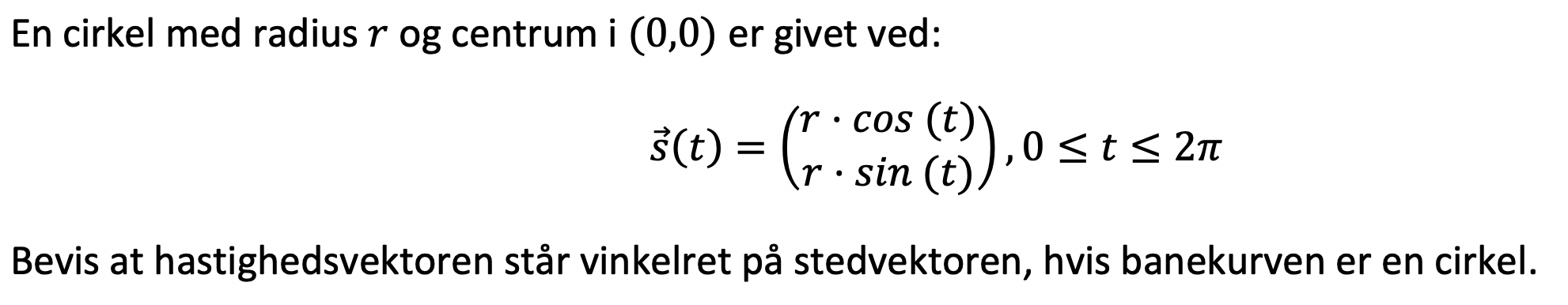Matematik

Bevis at en hastighedsvektor står vinkelret på en stedvektor i en cirkel

06. maj 2019 af Alexander231 - Niveau: A-niveau

Hejsa,

Jeg skal bevise at en hastighedsvektor står vinkelret på en stedvektor i en cirkel (opgaven er også vedhæftet som billede).

Jeg ved, at jeg skal bevise ortogonalitet, hvorfor bevisets betingelse må være s(t) * v(t) = 0, men efter at have differentieret stedvektoren og fundet prikproduktet til at være cos(t)^2*sin(t)^2 er jeg gået kold. Jeg har vist stirret mig blind på det, for jeg ved ikke, hvordan jeg fortsætter beviset herfra.

Krydser fingre for hjælp og tak på forhånd,

Vedhæftet fil: Skærmbillede 2019-05-06 kl. 13.19.12.png

Brugbart svar (1)

Svar #1
06. maj 2019 af mathon

Brugbart svar (3)

Svar #2
06. maj 2019 af mathon

$\small \overrightarrow{v}=\begin{pmatrix} -r\sin(t)\\ r\cos(t) \end{pmatrix}$

$\small \overrightarrow{s}\cdot \overrightarrow{v}=\begin{pmatrix} r\cos(t)\\r\sin(t) \end{pmatrix}\cdot \begin{pmatrix} -r\sin(t)\\r\cos(t) \end{pmatrix}=-r^2\sin(t)\cos(t)+r^2(\sin(t)\cos(t)=0$

Svar #3
06. maj 2019 af Alexander231

Pinligt... Jeg ser det nu... Tusind tak for hjælpen endnu en gang, Mathon! :-)

Brugbart svar (0)

Svar #4
04. maj 2021 af peterbelli

Hej ved godt dette er et gammelt opslag men håber der er nogen derude.
Er der en der kan forklare netop disse beregninger som er vist. Altså fremgangsmåde.
Links til videoer, læsestof og andet bliver også taget imod så længe det har relavans for netop ovenstående emne. Tak på forhånd

Brugbart svar (1)

Svar #5
04. maj 2021 af OliverHviid

#4 Hvis man differentierer stedvektoren, så får man hastighedsvektoren. Desuden står to vektorer vinkelret på hinanden hvis deres skalarprodukt er lig 0. Derfor prikker man stedvektoren med hastighedsvektoren, og man ser så at deres skalarprodukt netop er lig 0 som betyder at hastighedsvektoren står vinkelret på stedvektoren. Hvis du har flere spørgsmål så bare spørg.

Brugbart svar (0)

Svar #6
04. maj 2021 af peterbelli

Når du skriver "Derfor prikker man stedvektoren med hastighedsvektoren" mener du så at man differentierer stedvektoren for at finde hastighedsvektoren?

Brugbart svar (0)

Svar #7
04. maj 2021 af peterbelli

Og mange tak for så hurtige svar det sætter jeg pris på!

Brugbart svar (0)

Svar #8
04. maj 2021 af peterbelli

Du mener gange selfølgelig.

Skriv et svar til: Bevis at en hastighedsvektor står vinkelret på en stedvektor i en cirkel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.