Matematik

Hvordan bestemmer jeg rumfanget?

20. oktober 2019 af Sofiehanw - Niveau: A-niveau

Jeg har uploadet et billede af sprgs. Det er b) som jeg har svært ved.

Jeg tror at den måde man løser det på er følgende:

$\pi \cdot \int_{0}^{4}\left (x ^{\frac{3}{2}} \right )^2 dx$

Passer det, eller er det et andet interval man bruger til det? Dog tror jeg at formlen er korrekt til at finde volumen.

Vedhæftet fil: spr.PNG

Brugbart svar (1)

Svar #1
20. oktober 2019 af SuneChr

Du skal sætte hele funktionen i anden, integrere over intervallet og derefter
fratrække rumfanget af den cylinder, der har radius 1 og højde 4.
# 2 Ja, h e l e funktionsforskriften.

Svar #2
20. oktober 2019 af Sofiehanw

Når du siger "hele funktionen" er det så $x^{\frac{3}{2}}+1$ du mener, eller hvilken en er funktionen så?

Svar #3
20. oktober 2019 af Sofiehanw

Ahh okay, så det må blive sådan her $\pi \cdot \int_{0}^{4}\left ( (x ^{\frac{3}{2}}+1 \right )^2 -\frac{64}{5}) dx$

På den måde?

Brugbart svar (0)

Svar #4
20. oktober 2019 af ringstedLC

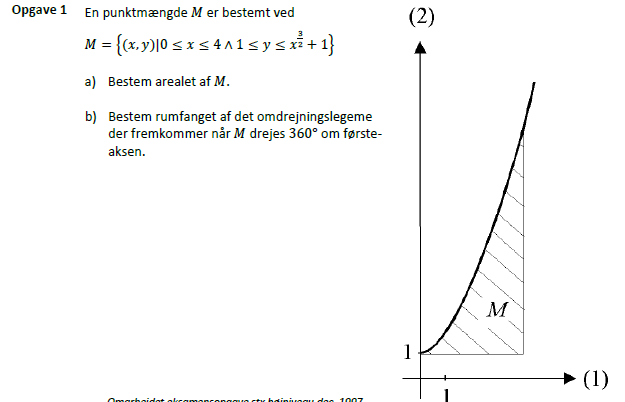
#0: Da dit forslag til metode ikke passer, er dit resultat i a) måske forkert.

Svar #5
20. oktober 2019 af Sofiehanw

#4 Virkelig? Altså ifølge facit så passer det, men det kan godt være at det bare er ved et uheld.

Måden jeg løste a) på er $\int_{0}^{4} x^\frac{3}{2} dx$ passer det?

Brugbart svar (1)

Svar #6
20. oktober 2019 af SuneChr

# 3
Nej.

Rumfang af M_{rotation x-akse} = $\pi \int_{0}^{4}\left ( x^{\frac{3}{2}}+1 \right )^{2} \textup{d}x\, \, -\pi \cdot 1^{2}\cdot 4$

Brugbart svar (0)

Svar #7
20. oktober 2019 af StoreNord

$\pi \cdot \int_{0}^{4}\left (x ^{\frac{3}{2}} \right )^2 dx \; \; \: \: \: \:$ $\: \: - \: \: \pi \cdot \int_{0}^{4}\left (1 \right )^2 dx$

Svar #8
20. oktober 2019 af Sofiehanw

Hvor får du $\pi * 1^2 * 4$ fra? #6

Svar #9
20. oktober 2019 af Sofiehanw

Er så måden jeg løste del a på forkert?

$\int_{0}^{4} x^\frac{3}{2} dx$

Brugbart svar (1)

Svar #10
20. oktober 2019 af SuneChr

# 9
Arealet af M er det, som du skriver i # 9, ja.
Ved rotation af M får man rumfanget af omtalte cylinder for meget med. Derfor må det for meget
trækkes fra, πr²h men må ikke komme ind under integraltegnet.

Svar #11
20. oktober 2019 af Sofiehanw

Ja okay det giver god mening #10

Jeg er bare lidt forvirret over at der står to forskellige beregninger op.

Altså #6 din er hvor den så er ganget med 4

Hvor imod #7 har en uden at gange den med 4

Hvorfor det? Hvilken en er den korrekte?

Okay jeg kan nu godt se at de begge giver det samme. Den ene er bare begranset i intervallet, hvorimod den anden ikke er, men derimod ganget med 4 (som jeg tror er h).

Tusind tak for hjælpen allesammen!! :)

Brugbart svar (0)

Svar #12
20. oktober 2019 af StoreNord

#9
For at finde arealet af M skal du integrere f fra 0 til 4, og derfra trække integralet af 1 fra 0 til 4.

Brugbart svar (0)

Svar #13
20. oktober 2019 af ringstedLC

#9
Er så måden jeg løste del a på forkert?

$\int_{0}^{4} x^\frac{3}{2} dx$

Både ja og nej. Ved at bestemme arealet med den metode undgår du at skulle fratrække arealet af M_Cyl. fordi du integrerer som om M "står" nede på x-aksen. Alternativet:

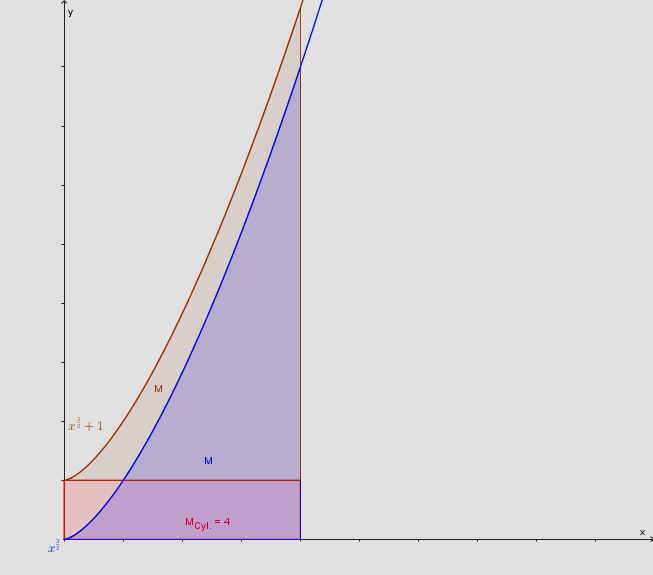
$\begin{align*} A_M &= \int_{0}^{4}x^{\frac{3}{2}}+1\,dx-\int_{0}^{4}1\,dx \\ &= \int_{0}^{4}x^{\frac{3}{2}}\,dx\end{align*}$

giver det samme pga. differensreglen. Men når du så skal finde et omdrejningslegeme, må du ikke "bare" integrere summen i anden og så gange med π. Legemet der ikke "står" på x-aksen, er større end det, der er afgrænset af x-aksen, derfor:

$\begin{align*} Vol_M &= \pi\cdot \int_{0}^{4}\left (x^{\frac{3}{2}}+1 \right )^2\,dx-\pi\cdot \int_{0}^{4}(1)^2\,dx \\ &= \pi\cdot \left (\int_{0}^{4}\left (x^{\frac{3}{2}}+1 \right )^2\,dx- \int_{0}^{4}(1)^2\,dx \right ) \end{align*}$

Den omtalte cylinder er det samme som:

$\begin{align*} Vol_{Cyl.} &= \pi\cdot \int_{0}^{4}(1)^2\,dx \\ &= \pi r^2h \;,\;r=1\;,\;h=4 \end{align*}$

Vedhæftet fil:__0.png

Skriv et svar til: Hvordan bestemmer jeg rumfanget?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.