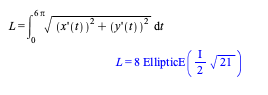Matematik

Bestemme den største lodrette afstand og Benyt modellen til at bestemme længden af randen af det indre af forbrændingskammeret.

14. februar 2020 af Cerlog - Niveau: A-niveau

Hej alle sammen, kan i hjælpe mig med at løse den her opgave? Jeg vil bare ikke hvordan skal jeg starte.

Vedhæftet fil: Annotation 2020-02-14 094547.png

Brugbart svar (0)

Svar #1
14. februar 2020 af mathon

Brugbart svar (0)

Svar #2
14. februar 2020 af mathon

a) den lodrette afstand d bestemmes af andenkoordinaten $\tfrac{1}{2}\cdot \sin(t)+\tfrac{7}{2}\cdot \sin(\tfrac{1}{3}\cdot t)$

Beregn differencen mellem dens maksimale og og minimale værdi.

Brugbart svar (0)

Svar #3
14. februar 2020 af mathon

korrektion:

a) Tidspunktet for den lodrette afstand d bestemmes af andenkoordinaten $\tfrac{1}{2}\cdot \sin(t)+\tfrac{7}{2}\cdot \sin(\tfrac{1}{3}\cdot t)$

Beregn differencen mellem dens maksimale og og dens "underliggende" værdi til samme tidspunkt.

Brugbart svar (0)

Svar #4
14. februar 2020 af AMelev

Definer y(t) := $\tfrac{1}{2}\cdot \sin(t)+\tfrac{7}{2}\cdot \sin(\tfrac{1}{3}\cdot t)$ . Bestem max og min på sædvanlig vis og beregn differensen.
På grund af symmetrien kan du også bare beregne d = 2·max.

Ad #3 Min og max indtræder på forskellige tidspunkter.

Brugbart svar (0)

Svar #5
14. februar 2020 af mathon

Selvfølgelig har #4 ret i, at
dét med samtidigheden var 'noget gedigent sludder'.

Brugbart svar (0)

Svar #6
09. maj 2020 af MARIOO123

Jeg har forsøgt at løse spørgsmål b, men kan ikke helt få maple til at fungere. Nogen der ved hvorfor jeg får svaret til EllipticE?

Vedhæftet fil:Skærmbillede 2020-05-09 kl. 15.43.21.png

Brugbart svar (1)

Svar #7
09. maj 2020 af ringstedLC

$\begin{align*} x'(t) &= \bigl ( \tfrac{1}{2}\cos(t)+\tfrac{7}{2}\cos\left (\tfrac{1}{3}t \right ) \bigr )' \\ y'(t) &= \bigl ( \tfrac{1}{2}\sin(t)+\tfrac{7}{2}\sin\left (\tfrac{1}{3}t \right ) \bigr )' \\ \end{align*}$

Brugbart svar (0)

Svar #8
09. maj 2020 af MARIOO123

Jeg har nemlig defineret x'(t) og y'(t), men det fungere heller ikke

Vedhæftet fil:Skærmbillede 2020-05-09 kl. 17.03.09.png

Brugbart svar (0)

Svar #9
09. maj 2020 af ringstedLC

Prøv lige at indstille til numerisk resultat. L = 23.01 cm.

Brugbart svar (0)

Svar #10
09. maj 2020 af MARIOO123

Mener du sådan?

Vedhæftet fil:Skærmbillede 2020-05-09 kl. 17.50.06.png

Brugbart svar (1)

Svar #11
09. maj 2020 af ringstedLC

Nej, det var bare for at give dig min CAS's resultat. Den giver nemlig "?" ved eksakt beregning og derfor foreslog jeg #9. Du skal ikke ændre noget i indtastningen, blot indstille til numerisk beregning/resultat.

Brugbart svar (0)

Svar #12
16. maj 2020 af Homework101

Nogen der kan forklare det for de helt dumme... forstår ikke helt, hvordan man finder maksimum

Brugbart svar (0)

Svar #13
16. maj 2020 af AMelev

#12 Som ved alle andre funktioner: Nulpunkter og fortegn for f ' "oversat" til nonotoni for f (monotonilinje).

Skriv et svar til: Bestemme den største lodrette afstand og Benyt modellen til at bestemme længden af randen af det indre af forbrændingskammeret.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.