Matematik
Vindskæv linkerne i Rummet
Hej
kan to linjerne som vindskæve i rummet danner en vinkel med hinanden ?
Svar #1
04. april 2020 af Festino
Ja, du kan finde vinklen ud fra prikproduktet af de to linjers retningsvektorer. For eksempel danner enhver lodret linje en vinkel på 90 grader med x-aksen.
Svar #2
04. april 2020 af DeepOcean
vindskær betyder ikke at de ikke skære hinanden og de er ikke parallel..så hvordan kan de danne vinklen med hinanden?
jeg har to vindskæv linjerne med retnongvektor er r1:(2,3,5) og r2:(-1,6,10) ..
jeg kan ikke finde vinklen mellem dem? kan i det ?
Svar #3
04. april 2020 af Festino
Kan vi ikke blive enige om, at man kan have en vandret og en lodret linje, som ikke skærer hinanden? Er det ikke rimeligt at sige, at vinklen imellem dem er ? Under alle omstændigheder må det være rimeligt at definere vinklen mellem to rette linjer som vinklen mellem deres retningsvektorer. Da
,
er
.
Svar #4
04. april 2020 af Eksperimentalfysikeren
Givet to vindskæve linier. Der findes en plan, der indeholder den ene linie, men er parallel med den anden. Den anden linie parallelprojiseres over i denne plan. Derved fremkommer en ny linie. Vinklen mellem den og den linie, der ligger i planen i forvejen, er den samme som vinklen mellem de to vindskæve linier.
Antag, at de to linier har retningsvektorer u og v. Planen lægges så den indeholder linien med retningsvektor u. Ved projektionen af den ande linie får man en ny linie med retningsvektor v.
Svar #6
04. april 2020 af BoHTX
Det forstår jeg ikke.
Du siger at der er to planer der er parallele og hver indeholder en linje. Men kun hvis den ene linje parallelprojiseres over på den anden plan, kan man danne en vinkel.
Men projektionen og den oprindelig linje er ikke den samme. Eller er linjer det samme som vektorer?
Svar #7
04. april 2020 af ringstedLC
#3Kan vi ikke blive enige om, at man kan have en vandret og en lodret linje, som ikke skærer hinanden? Er det ikke rimeligt at sige, at vinklen imellem dem er
?
Ikke enig: Lodret og vandret er kun entydigt bestemt i et punkt.
En vinkel har et toppunkt og derfor må linjer skære hinanden, for at man kan tale om vinklen mellem dem.
Og måske derfor svarer min CAS (GeoGebra) også med "?" på vinklen mellem to vindskæve linjer.
Svar #8
04. april 2020 af Capion1
Som et anskueligt eksempel på indbyrdes vindskæve linjer kan nævnes diagonalen i låget og en sidelinje i bunden af en almindelig kasse.
Vi kan tage en æske Tordenskjold-tændstikker. Læg en diagonal gennem søhelten og kig på f.eks.
æskens længste side i bunden.
Svar #10
04. april 2020 af Eksperimentalfysikeren
Tænk på et rektangulært bord, der står på et plankegulv, så det ene ben står på grænsen mellem to gulvbrædder. Bordet er drejet, så ingen de andre ben står på samme grænse. Linien m er den bordkant, der går fra det omtalte ben og i bordets længderetning. Linien n er grænsen mellem gulvbrædderne. m passerer endnu et ben. Nede på gulvet er der en linnie p mellem de to ben. Det er m's lodrette projektion på gulvet. Den danner en vinkel v med linien n. Denne linie er ogs vinklen mellem m og n. Læg mærke til, at det ben, der forbinder m med n, står vinkelret på begge de to linier.
Svar #11
04. april 2020 af Eksperimentalfysikeren
Lidt mere om bordeksemplet:
Lægges en plan gennen n og bordbenet, vil vinklen mellem denne plan og m også være v.
Hvis u er retningsvektor for m og w retningsvektor for n, u også retningsvektor for p, så man kan finde vinklen mellem m og n som vist i #3.
Svar #12
04. april 2020 af DeepOcean
Jeg mener for at man kan snakke om vinkel så skal vi har et bestem punkt spm kunde de to linjen sammen og når to linjer er vindskæv så har vi ikke en entydligt punkt som kan knunde dem samme og derfor har vi ikke nogen vinkel ,Lomme regne bekræfte teori og viser fejl ved indtastning af de to retningsvektorer.
Men tak for alle deltage i diskussion . Det er dejligt at man hører fra forskellige dygtigt matematiker.
Svar #13
04. april 2020 af ringstedLC
#12: Enig. Men vektorernes vinkel må ikke give fejl på CAS/lommeregner. Her kan vi jo finde to repræsentanter, der netop har et skæringspunkt og bestemme vinklen.
Svar #14
04. april 2020 af Eksperimentalfysikeren
#12 Hvordan definerer man så vinklen mellem to planer?
Man har udvidet den oprindelige definition fra vinkel mellem to linier i samme plan til toplanvinkler og vinkler mellem vindskæve linier.
Toplanvinkel: Hvis to planer skærer hinanden, er skæringen en ret linie, kaldet sporet. Der eksisterer en plan, der er vinkelret på denne linie. Den skærer de to første planer i to linier, der skærer hinanden i sporet af de to første planer. Vinklen mellem disse to linier kaldes toplanvinklen.
Vindskæve linier: Blandt de planer, der indeholder den ene linie, er der én, der er vinkelret på den anden. Det gælder også, hvis de to linier bytter rolle. Sporet mellem de to planer står vinkelret på begge linier. Toplanvinklen mellem de to planer er vinklen mellem de to vindskæve linier.
Du må aldrig lade dig snyde af lommeregnere. Der er mange af dem, der ikke virker i overensstemmelse med den matematiske tradition. Der er mange, der ikke kan finde ud af, hvilken rækkefølge, udregninger skal ske i.
Svar #15
04. april 2020 af Festino
#7 Geogebra kan sagtens finde vinklen mellem to vindskæve linjer.
#12 Jo, man kan godt definere vinklen mellem to vindskæve linjer. Vinklen er defineret som vinklen mellem linjernes retningsvektorer. Hvis din lommeregner viser fejl, når du forsøger at finde vinklen mellem de to retningsvektorer, så må du have gjort et eller andet forkert.
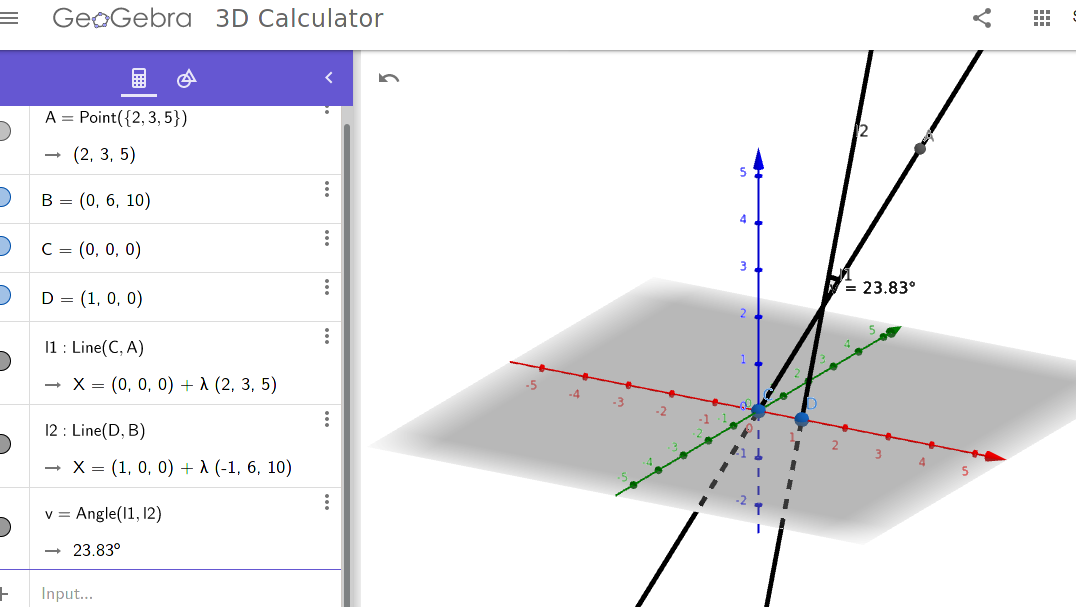
Svar #17
05. april 2020 af Festino
#16 Hvad får dig til at tro, at linjerne ikke er vindskæve? Mener du, at de er parallelle, eller mener du, at de skærer hinanden? Ingen af delene er tilfældet, og derfor er linjerne vindskæve.
Svar #18
05. april 2020 af Eksperimentalfysikeren
Linierne skærer hinanden i (4/5,6/5,2). GeoGebra kan ikke finde vinklen mellem to vindskæve linier.
Det betyder dog ikke, at man ikke kan have en vinkel mellem to vindskæve linier. Det er udelukkende et spørgsmål om, hvordan man definerer den. Hvis man definerer den som vinklen mellem retningsvektorerne, har det den fordel, at definitionen også gælder i højere dimensioner. Ved regressionsanalyse beregner man også en korellationskoefficient. Det er faktisk cosinus til vinklen mellem to vindskæve linier i et n-dimensionalt rum.
Skriv et svar til: Vindskæv linkerne i Rummet
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







