Matematik

Endnu engang hjælp til trigonomitri

23. juni 2020 af Jensxxx - Niveau: C-niveau

Hej,

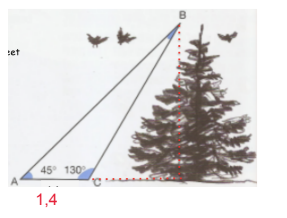
Jeg skal finde højden i træet med vinklerne og sidelængden givet i den vedhæftede tegning, men har ingen annelse hvordan jeg skal komme videre.

Vedhæftet fil: trigo.png

Brugbart svar (0)

Svar #1
23. juni 2020 af Soeffi

Se evt. https://www.studieportalen.dk/forums/thread.aspx?id=1885469.

Brugbart svar (0)

Svar #2
23. juni 2020 af mathon

$\small \begin{array}{lllll} h=\frac{\tan(45\degree)\cdot \tan(130\degree)}{\tan(45\degree)+ \tan(130\degree)}\cdot \left ( 1.4\;m \right ) \end{array}$

Brugbart svar (0)

Svar #3
23. juni 2020 af mathon

korrektion:
$\small \small \begin{array}{lllll} h=\frac{\tan(45\degree)\cdot \tan(50\degree)}{\tan(45\degree)+ \tan(50\degree)}\cdot \left ( 1.4\;m \right ) \end{array}$

Svar #4
23. juni 2020 af Jensxxx

kunne man også evt. bruge sinusrelationerne til at finde det rigtige svar?

Brugbart svar (0)

Svar #5
23. juni 2020 af mathon

Ja.

Brugbart svar (0)

Svar #6
23. juni 2020 af Soeffi

#4 kunne man også evt. bruge sinusrelationerne...?

Jo, du kan bruge sinusrealtionerne til at finde |BC|. Derefter kan du finde højden, h, ved hjælp af formlen:

$h=|BC|\cdot sin(180^o-C)=|BC|\cdot sin(C)$

Sinusrelatoinerne giver:

$|BC|/sin(A) = |AC|/sin(B) \Rightarrow |BC| = |AC|\cdot sin(A)/sin(B)$

Reglen om, at vinkelsummen i en trekant er 180°, giver: vinkel B = 180° - 45° - 50° = 5°. Dvs.

$h = (|AC|\cdot sin(A)/sin(B)) \cdot sin(C) =$

$|AC|\cdot sin(A)\cdot sin(C)/sin(B) =$

$1,4\cdot sin(45^o)\cdot sin(130^o)/sin(5^o)=8,701$

PS: #3 skal være:

$h=1,4\cdot \frac{tan(45^o) \cdot tan(50^o)}{tan(50^o)-tan(45^o)}=8,701$

Brugbart svar (0)

Svar #7
24. juni 2020 af mathon

kort:
$\small \begin{array}{llllll} \textup{med tangens:}\\& \begin{array}{llllll} h=\frac{\tan(50\degree)\cdot \tan(45\degree)}{\tan(50\degree){\color{Red} -} \tan(45\degree)}\cdot (1.4\;m) \end{array}\\ \textup{med sinus:}\\& \begin{array}{llllll} h=\frac{\sin(45\degree)\cdot \sin(50\degree)}{\sin(45\degree+130\degree)}\cdot (1.4\;m) \end{array} \end{array}$

Brugbart svar (0)

Svar #8
24. juni 2020 af Soeffi

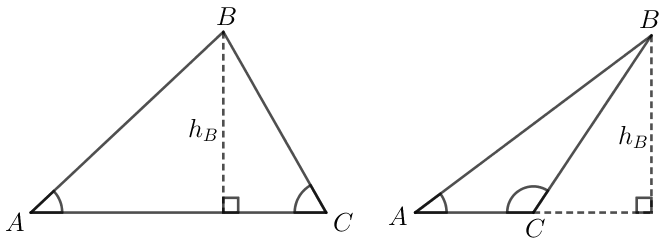
#1. Det er sådan set bare formlen for højden i B (h_B) for en trekant ABC, hvor længden af AC tillige med vinklerne A og C er kendte.

$h_B = |AC|\cdot sin(A)\cdot sin(C)/sin(A+C)$

Brugbart svar (0)

Svar #9
02. juli 2020 af Soeffi

#8.

Grundlæggende gælder, at

$h_B = |AB|\cdot sin(A)$

Kender man ikke |AB|, men derimod |AC| samt de hosliggende vinkler, så kan man finde |AB| ved en sínusrelation:

$|AB|/sin(C)=|AC|/sin(B)\Rightarrow$

$|AB|=|AC|\cdot sin(C)/sin(B)\Rightarrow$

$|AB|=|AC|\cdot sin(C)/sin(180^o-(A+C))\Rightarrow$

$|AB|=|AC|\cdot sin(C)/sin(A+C)$

Dette indsættes derefter i formlen for h_B og man får resultatet fra #8. Formlerne er de samme uanset om højden ligger indenfor eller uden for trekanten.

Vedhæftet fil:højde.png

Skriv et svar til: Endnu engang hjælp til trigonomitri

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.