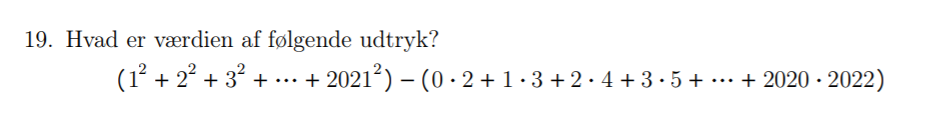Matematik

Georg Mohr opgave omkring et udtryk

21. november 2020 af Batsamyou - Niveau: A-niveau

Hej

Dette er en opgave, som var med i Georg Mohr konkurrencen i år. Jeg ved simpelthen ikke hvordan den kan løses. Nogle som man kan hjælpe? På forhånd takk :)) Opgaven er vedhæftet.

Vedhæftet fil: Georg mohr opgave.PNG

Brugbart svar (0)

Svar #1
21. november 2020 af Eksperimentalfysikeren

To tals sum gange de samme to tals differens.

Svar #2
21. november 2020 af Batsamyou

Det forstår jeg ikke

Svar #3
21. november 2020 af Batsamyou

Kan du forklare det lidt mere detaljeret?

Svar #4
21. november 2020 af Batsamyou

Jeg ved at resultatet er 2021, men ved ikke helt hvordan man er kommet frem til det

Brugbart svar (0)

Svar #5
21. november 2020 af Soeffi

#0.

$\sum_{n=1}^{2021}n^2-(n-1)\cdot (n+1)=\sum_{n=1}^{2021}n^2-(n^2-1)=\sum_{n=1}^{2021}1=2021$

Brugbart svar (0)

Svar #6
21. november 2020 af ringstedLC

#3
Kan du forklare det lidt mere detaljeret?

Det er en kvadratsætning:

$\begin{align*} n^2-\bigl(n^2-1^2\bigr) &= \\ n^2-\bigl((n-1)\cdot (n+1)\bigr) &= 1 \\ 1^2-\bigl((1-1)\cdot (1+1)\bigr) &= \\ 1^2-\bigl(0\cdot 2\bigr) &= 1 \\ ... \\ 2021^2-\bigl((2021-1)\cdot (2021+1)\bigr) &= \\ 2021^2-\bigl(2020\cdot 2022\bigr) &= 1 \end{align*}$

Brugbart svar (0)

Svar #7
21. november 2020 af Soeffi

#5.

$\\(1^2+2^2+3^2+...+2021^2)-(0\cdot 2+1\cdot 3+2\cdot 4+...+2020\cdot 2022)=$

$\sum_{n=1}^{2021}n^2-\sum_{n=1}^{2021}(n-1)\cdot (n+1)=\sum_{n=1}^{2021}n^2-(n-1)\cdot (n+1)=$

$\sum_{n=1}^{2021}n^2-(n^2-1)=\sum_{n=1}^{2021}1=2021$

Brugbart svar (0)

Svar #8
21. november 2020 af Capion1

# 4
Bemærk sidste linje i # 7:

$\sum_{n=1}^{2021}1=1+1+1+...+1\: \: (2021\, \, addender)$
men ikke

$\sum_{n=1}^{2021}n=1+2+3+...+2021$
Her er der også 2021 addender, men summen en helt anden.

Brugbart svar (0)

Svar #9
22. november 2020 af Anders521

#0 Jeg havde ikke lige gennemskuet det andet led kunne skrives som Σ_k=1 ²⁰²¹(k+1)·(k-1). Alternativ kan man gøre flg.:

( 1² + 2² + 3² + ^... + 2021²) - ( 0·2 + 1·3 +2·4 +3·5 + ^... + 2020·2022 ) = ( 1² + 2² + 3² + ^... + 2021² ) - ( 0·(0+2) + 1·(1+2) + 2·(2+2) + 3·(3+2) + ^...+ 2020·(2020+2) ) = ( 1² + 2² + 3²+^... + 2021² ) - ( 0² + 0 + 1² + 2 + 2² +4 + 3² +6 +^... + 2020² + 4040 ) = ( 1² + 2² + 3²+^...+2021² ) - (1² + 2² + 3² + ^... + 2020² + 2 + 4 + 6 + ^... + 4040 ) = 2021² - ( 2 + 4 + 6 +^... + 4040 ) = 2021² - ( 2·( 1 + 2 + 3 + ^...+ 2020 )) = 2021² - ( 2·[ 2020·( 2020 + 1 )/2 ) = 2021² - ( 2020² + 2020 ) = ( 2021² - 2020² ) - 2020 = ( 2021 + 2020 )·( 2021 - 2020 ) - 2020 = 4041 - 2020 = 2021.

Skriv et svar til: Georg Mohr opgave omkring et udtryk

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.