Ledetråd ønskes 😊

Uh, det var en rigtig morsom opgave, - og udfordrende.
Den kaster jeg mig over med det vons.... :-)

Jeg skal lige forstå det ret, - er det lige meget hvilket ciffer, der fjernes?

Man kan overveje:
Lad det femcifrede tal ha' cifrene
   a₄a₃a₂a₁a₀
hvor man først fjerner cifret a₀
Da har vi:

10000a₄ + 1000a₃ + 100a₂ + 10a₁ + a₀
+
1000a₄ + 100a₃ + 10a₂ + a₁
=
52713

Efterfølgende forsøg ved at fjerne a₁ , ... , a₄
indtil summen er, hvad den skal være. 

Man kan lade et lille EDBprogram gennemløbe mulighederne og udfinde de fem cifre.

#0. Du starter med at indse, at det er sidste ciffer, der skal slettes, ellers kan summen ikke blive ulige. Dette fører til, at de to sidste cifre i det femcifrede tal er "12" eller "21", da deres sum er 3.

I forlængelse af #6

Det første ciffer (i det femcifrede tal) må vel nødvendigvis være 4 eller 5

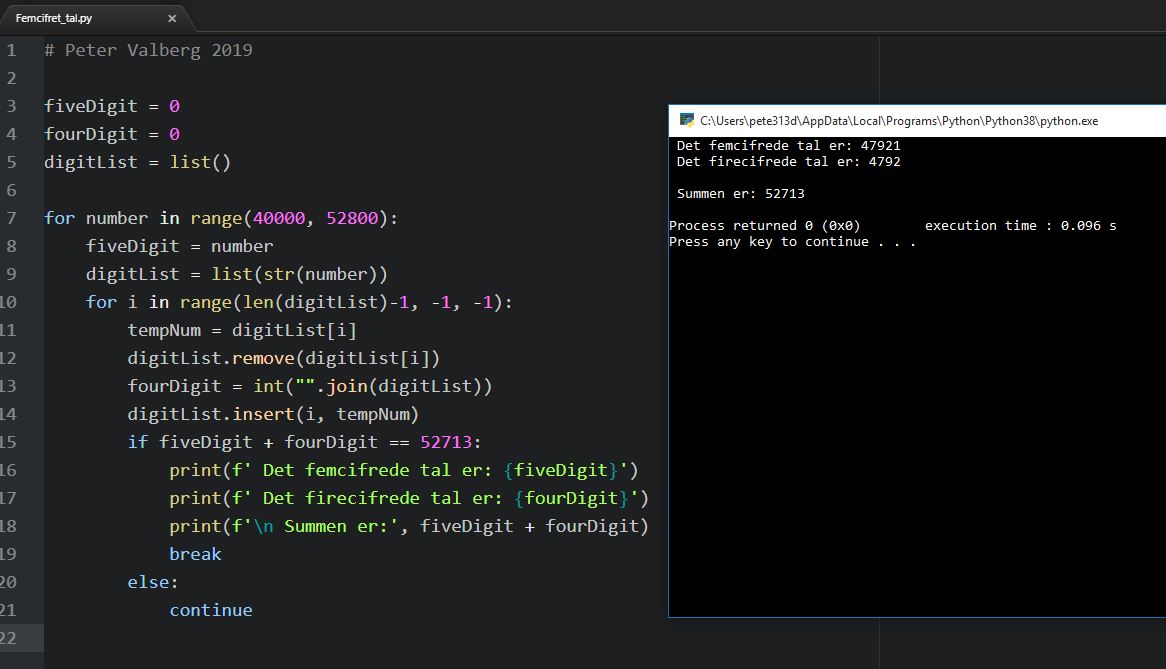
Som SuneChr i #6 er inde på, så kan man skrive et lille program,
der afprøver alle mulighederne (mellem fx 40000 og 52800)...
Der står jo ikke noget i opgaven om, at man ikke må :-)

I forlængelse af #7...
Antag at de to sidste cifre i det femcifrede tal er "12". Dermed er sidste ciffer i det femcifrede tal 2 og sidste ciffer i det firecifrede tal 1. Summen af disse cifre er 3, som stemmer med sidste ciffer i 52713.

Kald det tredjesidste ciffer x. Næstsidste cifre i det femcifrede er "1" og næstsidste ciffer i det firecifrede tal er "x". Næstsidste ciffer i summen er 1 (52713). Man får følgende regnestykke for x: 1 + x = 1 ⇒ x = 0. De tre sidste cifre i det femcifrede tal er dermed: "012".

Dette fører til et tilsvarende regnestykke for andet ciffer (y) i det femcifrede tal: 0 + y = 7⇒ y = 7. De fire sidste cifre i det femcifrede tal er dermed: "7012".

Dette fører endelig til følgende regnestykke for første ciffer (z) i det femcifrede tal: 7 + z = 12 (2 med 1 in mente)⇒ z = 5. Man får samlet:

5 7 0 1 2 
+ 5 7 0 1
6 2 7 1 3  Dette ses at være forkert.

I stedet prøver man med "21" som de to sidste cifre og får med samme fremgangsmåde:

4 7 9 2 1
+ 4 7 9 2
5 2 7 1 3  Dette ses at være rigtigt.

#0 Nogle overvejelser omkring opgavens løsning er vedhæftet....