Matematik

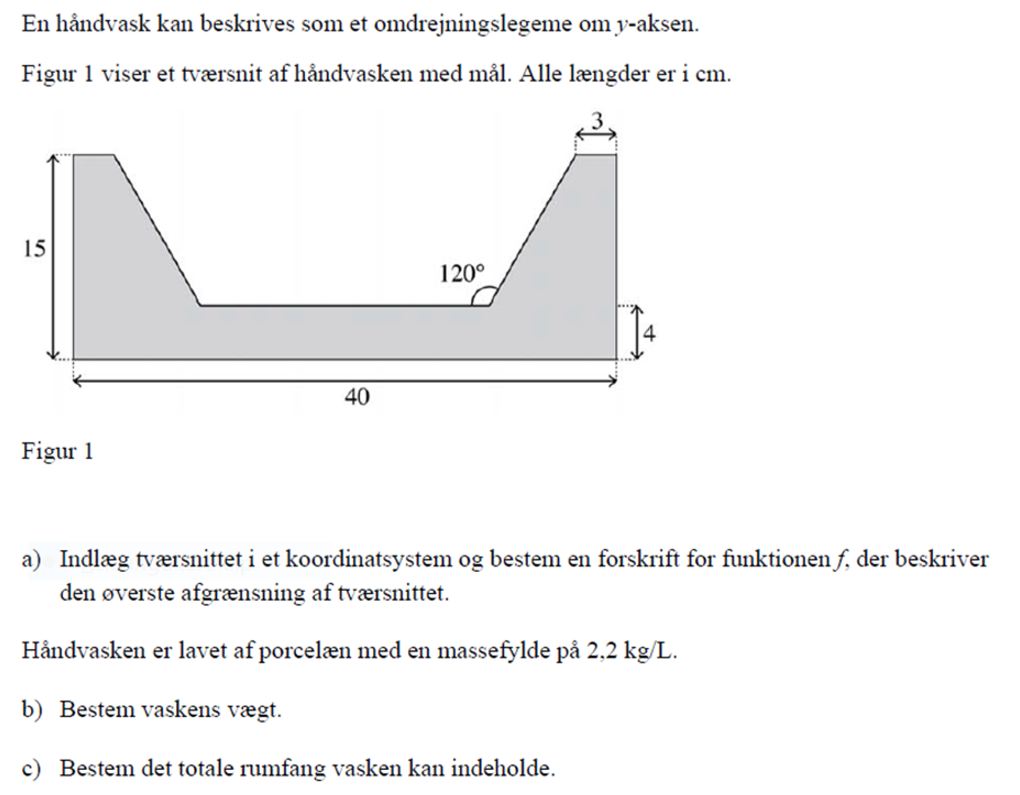
Vægt og rumfang

24. november 2019 af AmiraKh - Niveau: A-niveau

Hej, er der en venlig sjæl herinde som kan hjælpe mig med opgave b? Jeg skal beregne vaskens vægt, men jeg har ingen anelse om hvordan det skal gøres..

Jeg håber at kunne få noget hjælp :)

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
24. november 2019 af ringstedLC

$\begin{align*} m_{vask} &= \rho _{vask}\cdot V_{vask} \\ m_{vask} &= \rho _{vask}\cdot \left (V_{cyl.}-V_{keglestub}\right ) \end{align*}$

Brugbart svar (0)

Svar #2
24. november 2019 af SuneChr

Opgaven ville, på A-niveau, have været mere udfordrende, hvis overgangen fra bunden af vasken
op til øverste kant havde form af en ikke-lineær kurve.
Det kunne se ud, som der lægges op til beregning v.h.a. integralregning, men som det beskrives nederst
i # 1, er det en lettere vej at gå ved at kunne indse, at der er to kendte legemer, man let finder rumfanget af.

Brugbart svar (0)

Svar #3
24. november 2019 af Eksperimentalfysikeren

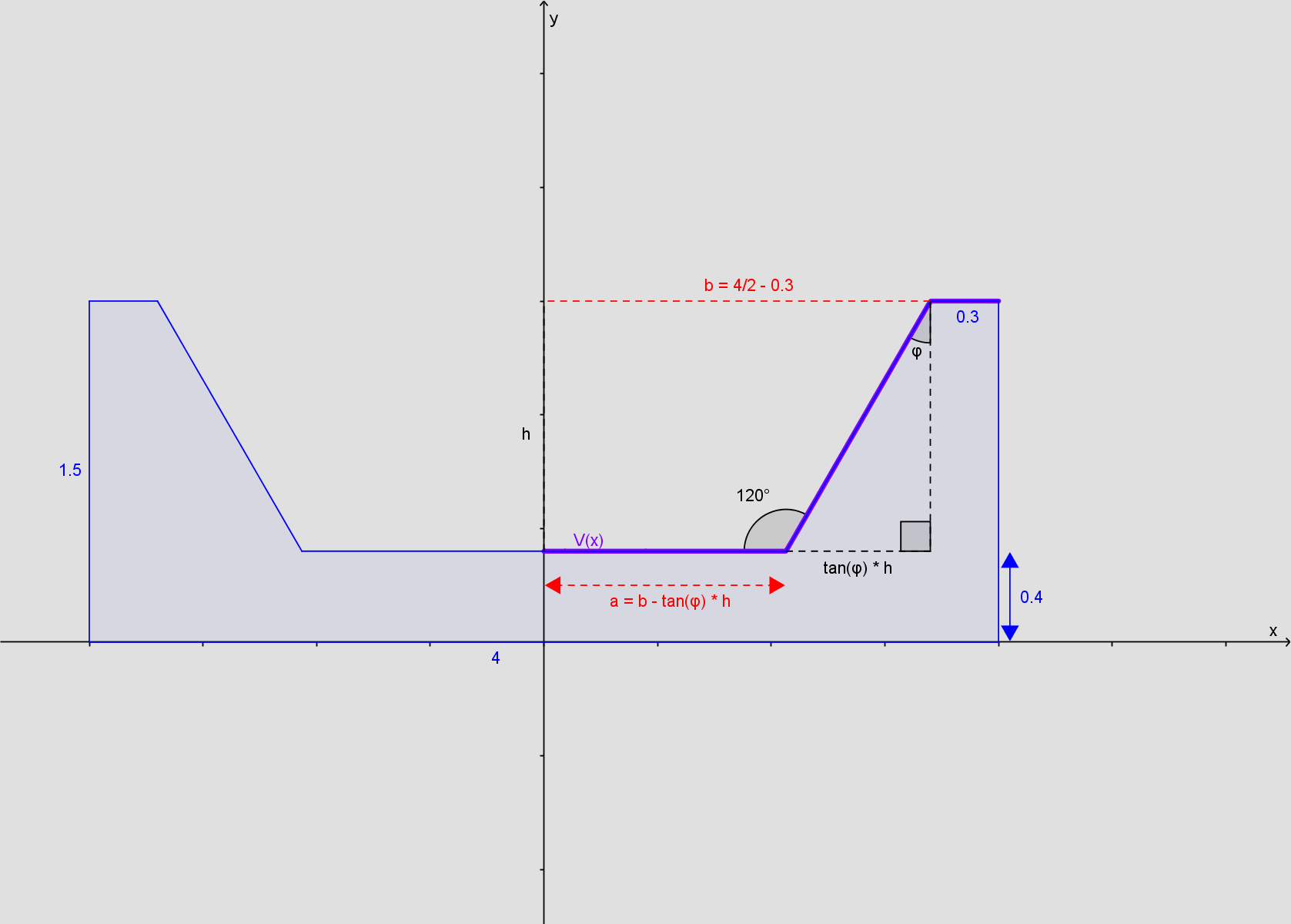
a) Jeg antager, at x-aksen ligger langs undersiden. f er en stykkevis lineær funktion, der er symmetrisk om y aksen, så det er nok at se på forløbet for x>=0. Det kan så spejles bagefter.

Der er fire punkter, der deler funktionen i de lineære dele. A ligger på y-aksen (x=0). B ligger der, hvor der er vist 120 grader. C ligger der, hvor funktionen igen bliver konstant, og D er slutpunktet. Du skal finde koordinaterne til disse punkter. A, C og D giver ikke de store problemer. Ved B skal du finde hældningen af liniestykket BC. Det kan du finde ud fra den vinkel, liniestykket danner med x-aksens positive retning. Den vinkel, der er vist er ud fra x-aksens negative retning.

Når du har hældningskoefficienten, kan du finde ligningen for liniestykket og dermed for x-koordinaten for B.

Herefter vil jeg anbefale, at du går til spørgsmål c). Her er der tale om en keglestub, hvor du af oplysningerne fra a) kan finde radierne i endefladerne og højden. Du slår formlen for rumfanget af en pyramidestub op og indsætter.

b) Brug metoden i #1, idet du nu har en del af svaret i c).

Svar #4
24. november 2019 af AmiraKh

Tak for hjælpen :)

Brugbart svar (0)

Svar #5
24. november 2019 af ringstedLC

b) Start med at omregne målene til dm, så de passer til L.

$\begin{align*} m_{vask} &= \rho _{vask}\cdot \left (V_{cyl.}-V_{keglestub}\right ) \\ V_{cyl.} &= \pi r^2h \\ V_{cyl.} &= \pi\cdot \left (\tfrac{4}{2}\right )^2\cdot 1.5\;\left ( dm^2\cdot dm=L \right )=6\pi\;(L)\approx18.85\text{ L} \\ V_{keglestub} &= \tfrac{1}{3}\pi h\cdot \left(a^2+b^2+ab\right) \\V_{keglestub} &= \tfrac{1}{3}\pi\cdot 1.1 \cdot \left((1.7-\tan(\varphi )\cdot 1.1)^2+1.7^2+(1.7-\tan(\varphi )\cdot 1.1)\cdot 1.7\right) \left (dm\cdot dm^2=L\right )=6.72\text{ L} \\ \rho _{vask} &= 2.2\;\left (\tfrac{kg}{L}\right ) \\ m_{vask} &= 2.2\cdot (18.85-6.72)\;\left ( \tfrac{kg\,\cdot \,L}{L} \right )= 26.68 \text{ kg} \end{align*}$ c) Med formlen for omdrejningslegeme omkring y-aksen:

$\begin{align*} V_{vask}(x) &= \left\{\begin{matrix} 0.4 &0\leq x\leq1.7-\tfrac{\sqrt{3}}{3}\cdot 1.1 \\ \sqrt{3}x-1.7\sqrt{3}+1.5 & 1.7-\tfrac{\sqrt{3}}{3}\cdot 1.1<x\leq 1.7 \\ 1.5 & 1.7<x\leq2 \end{matrix}\right. \\ Vol_{vask} &= 2\pi\cdot \left (\int_{0}^{2}x\cdot V_{cyl}(x)\,dx-\int_{0}^{2}x\cdot V_{vask}(x)\,dx \right ) \\ &= 2\pi\cdot \int_{0}^{2}x\cdot \left (1.5-V_{vask}(x)\right )\,dx\;(L) \\ Vol_{vask} &= 6.72\text{ L} \end{align*}$

Vedhæftet fil:A_M_080 - Omdrejningslegeme, vask_Sedanur.png

Skriv et svar til: Vægt og rumfang

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.